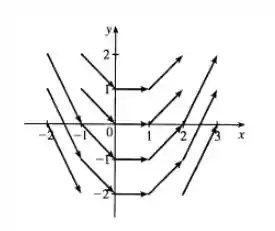
Esboce o campo vetorial , desenhando um diagrama como o da Figura ou da Figura .
Passo 1
Oi galera, tudo bem? Primeiro vamos começar vendo o tamanho desse vetor:
Passo 2
Quando é negativo, o vetor aponta na direção de negativo (para baixo). Quando é positivo, o vetor aponta para cima.
Sua componente horizontal é sempre constante e positiva, e vale . Então os vetores sempre apontam para a direção de positivo.
Quanto maior o valor de , mais comprido é o vetor.
Os vetores são tangentes à parábolas com boca para cima.
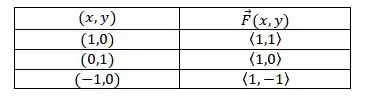
Vamos fazer uma tabela com alguns valores de e os respectivos vetores nesses pontos:
Num sistema cartesiano eles ficam assim ó:
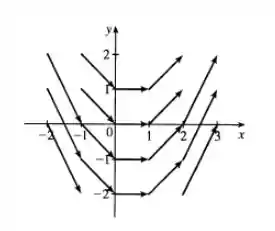
Resposta