Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.Revisão - Ex. 46

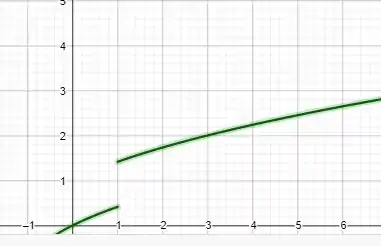
Esboce a curva e encontre a área total entre ela e o intervalo dado no e i x o   x .

y = x + 1 - 1   ,       [ - 1 ,   1 ]

Passo 1

A primeira coisa que faremos é analisar o ponto onde a função é nula, onde:

y = x + 1 - 1 = 0

Se:

x = 0

0 + 1 - 1 = 1 - 1 = 0

Agora, podemos subdividir nossa função em dois intervalos, de :

- 1 ≤ x ≥ 0   ( n e g a t i v o   e   à   e s q u e r d a )

0 ≤ x ≤ 1   ( p o s i t i v o   e   à   d i r e i t a )

Esses serão nossos limites de integração, reescrevendo a integral temos:

∫ - 1 1 x + 1 - 1   d x = - ∫ - 1 0 x + 1 - 1 d x + ∫ 0 1 x + 1 - 1 d x

Resolvendo a integral, temos:

∫ - 1 1 1 x 2 - 1   d x = - 2 ( x + 1 ) 3 / 2 3 - x - 1 0 + 2 ( x + 1 ) 3 / 2 3 - x 0 1

∫ - 1 1 x + 1 - 1   d x = 4 3 ( 2 - 1 )  

Passo 2

Esboçando a função, percebemos que ela é contínua de -1 até 0, se torna descontínua, e retorna a ser contínua em 0 até 1.

Resposta

∫ - 1 1 x + 1 - 1   d x = 4 3 ( 2 - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a área da região” triangular” no primeiro quadrante, limitada acima pela curva y = e x 2 abaixo pela curva y = e - x 2 e à direita pelas curva y = 2 l n ( 2 )
Determine a área das regiões compreendidas entre y = s e n ( π x 2 ) e y = x
Determine a área da região” triangular” no primeiro quadrante, limitada acima pela curva y = e 2 x , abaixo pela curva y = e x e à direita pelas curva y = l n ( 3 ) .
Determine a área da região no primeiro quadrante, limitada à esquerda pelo eixo y , abaixo pela reta y = x 4 , acima à esquerda pela curva y = 1 + x e acima à direita pela curva y = 2 x .
Determine a área das regiões compreendidas entre y = c o s ( π x 2 ) e y = 1 - x 2