Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar a curva que tem as equações paramétricas dadas por:
Bom, para fazer isso, vamos atribuir alguns valores a , marcar os pontos obtidos no gráfico e verificar a forma da nossa curva.
Vamos lá!
Passo 2
Como nosso intervalo vai de a , vamos verificar o valor de e nesses pontos, fazendo:
E
Então, nosso gráfico vai do ponto até o ponto .
Passo 3
Agora vamos atribuir outros valores a .
Para , temos:
Aí obtemos o ponto .
Para , temos:
Então, obtemos o ponto .
Para , temos:
E obtemos .
Para , temos:
E obtemos .
Passo 4
Aqui já conseguimos perceber que o menor valor de no intervalo é , no ponto . Além disso, repare que conforme cresce, o cresce lentamente de até . E o desce até e depois sobe até .
Assim, já podemos marcar nosso pontos no plano cartesiano e liga-los para obter a curva:
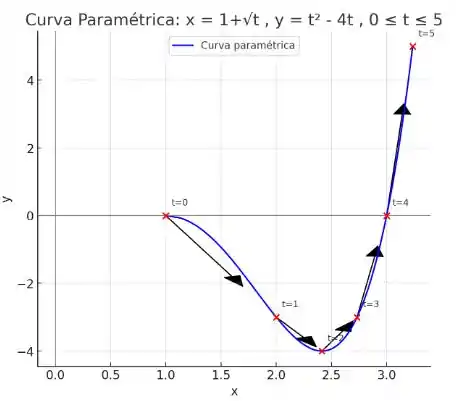
Observe que a direção da curva é dada pelas setas, começando no ponto , depois desce e passa por e chega ao ponto mais baixo . Depois sobe de volta passando por e termina em .
Valeu, galera! Até a próxima! 😉
Resposta