Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 12
Esboce o gráfico da função e use-o para determinar os valores de para os quais existe.
Passo 1
Falaaaaaa aí, belezinha?? Bom... a questão nos dá a seguinte função :
Essa é uma função definida por partes, então pra esboçar o gráfico, nós vamos pegar os 3 gráficos das 3 funções e junt-alos nos seus respectivos intervalos.
Depois vamos usar esse gráfico pra determinar os valores de para os quais o seguinte limite existe:
Pra que um limite exista num ponto , precisamos que os limites laterais sejam iguais nesse ponto. Em outras palavras, o limite pela esquerda precisa ser igual ao limite pela direita:
Lembrando que limite lateral é um limite calculado considerando a aproximação do ponto apenas por um lado (valores maiores ou menores que ele). Mas vamos ver melhor isso depois.
E aí?? Bora lá??!! 😉
Passo 2
Com o auxilio do GeoGebra, vamos ver os gráficos de e que já são funções bem conhecidas:
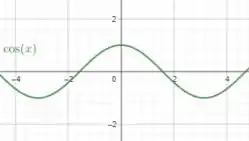
Pra obter o gráfico de , basta adicionar 1 a todos os valores da função, ou seja, desloca-la pra cima em 1 unidade:
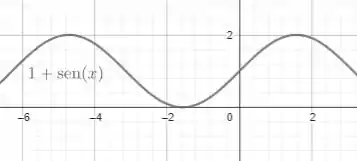
Agora pegando cada um deles nos intervalos dados pelo enunciado:
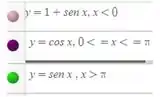
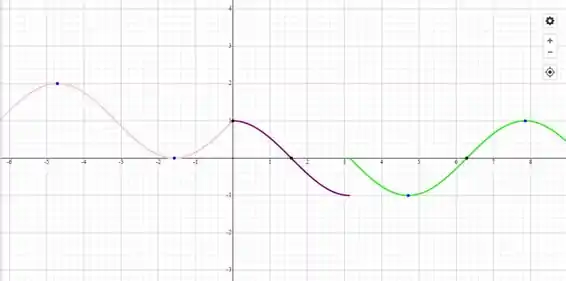
Passo 3
Como já introduzimos no passo 1, para que um limite exista precisamos que os limites laterais (limite à direita e limite à esquerda) sejam iguais. O limite à direita de quando se aproxima de pela direita e o limite à esquerda de quando se aproxima de pela esquerda devem ambos existir e serem iguais.
CUIDADO! Não tem problema se a função não for contínua naquele ponto, ou seja, se o valor da função for diferente do limite. Apenas precisamos que o limite exista.
Vamos olhar o gráfico!
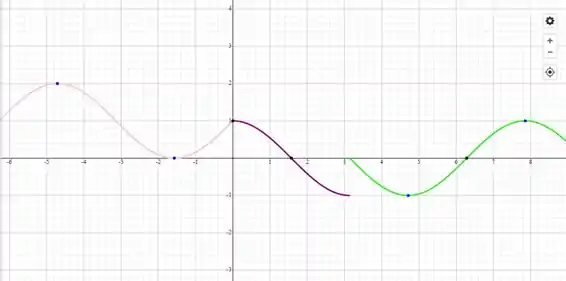
Como podemos ver, as 3 funções são contínuas (funções seno e cosseno são contínuas) e o limite existe em todos os pontos pra cada trecho.
Os pontos que desconfiamos são os pontos de ligação, ou seja
Em , na junção da curva rosa com a curva roxa no entanto, temos continuidade. Se nos aproximamos do ponto pela direita ou pela esquerda, chegamos no mesmo lugar. Então nesse ponto o limite existe.
Já no ponto , entre as curvas roxa e verde, claramente temos um salto.
- Vindo pela direita (curva verde), a função se aproxima do valor
- Vindo pela esquerda (curva roxa), a função se aproxima de
Então, como os limites laterais são diferentes, o limite geral não existe neste ponto.
Concluindo, o existe para todos os valores de exceto para
Resposta
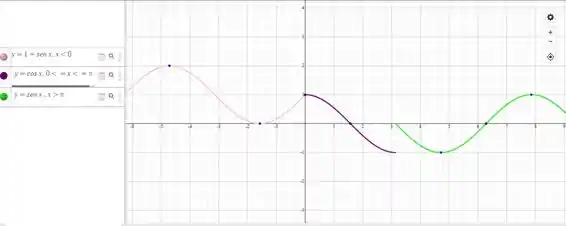
O existe para todos os valores de exceto para