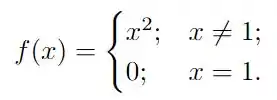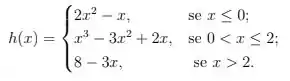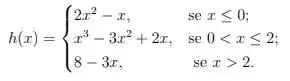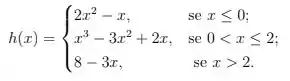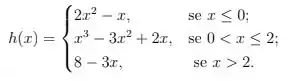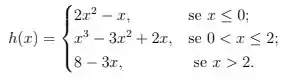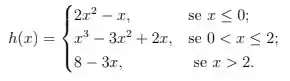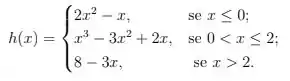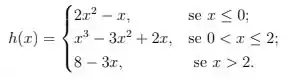Exercícios de Limites Laterais e Existência do Limite - Lista de Exercícios Resolvida
Questão 1
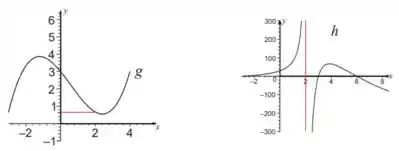
Dadas as duas funções abaixo:
Calcule os limites laterais dados abaixo e verifique se o limite existe, comparando os limites laterais:
, , onde:
, , onde:
Ver solução completaQuestão 4
Considere a função definida pelo gráfico abaixo.
Determine o para se existir
Ver solução completaQuestão 7
Esboce o gráfico da função a seguir e use-o para determinar os valores de para os quais
existe:
Ver solução completaQuestão 9
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(c)
Ver solução completaQuestão 10
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(a)
Ver solução completaQuestão 19
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 24
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 31
5. Encontre, quando existir, o limite. Caso não exista, explique por quê.
c.
Ver solução completaQuestão 33
1b) Calcule os seguintes limites. Não é permitido o uso da regra de L’Hôspital:
Ver solução completaQuestão 38
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 39
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 44
Calcule, se existir, o valor dos seguintes limites. Caso não exista, justifique.
Ver solução completaQuestão 47
5. Encontre, quando existir, o limite. Caso não exista, explique por quê.
c.
Ver solução completaQuestão 53
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Questão 55
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 82
Sem usar a regra de L’Hospital, calcule o limite ou prove que não existe:
Ver solução completaQuestão 84
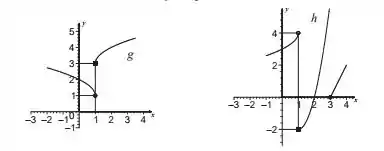
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
E
ambas no ponto
Questão 85
Se para todo e , verifique se as afirmativas abaixo são verdadeiras ou falsas. Caso seja verdadeira, apresente uma justificativa. Caso seja falsa, apresente um contraexemplo.
(a) não existe
(b)
(c) Se existir, é positivo
Ver solução completaQuestão 92
6) Sem utilizar a regra de L’Hôpital, calcule os limites abaixo ou justifique caso os mesmos não existam:
a)
Ver solução completaQuestão 93
6) Sem utilizar a regra de L’Hôpital, calcule os limites abaixo ou justifique caso os mesmos não existam:
b)
Ver solução completaQuestão 94
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
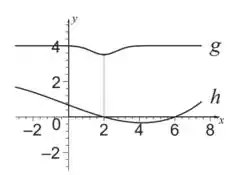
Questão 95
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
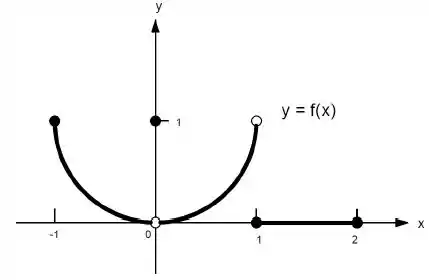
a)
Ver solução completaQuestão 98
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
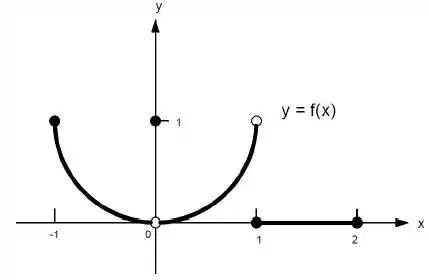
b)
Ver solução completaQuestão 99
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
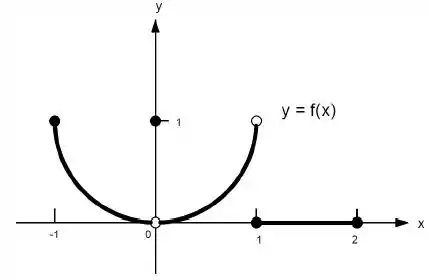
d)
Ver solução completaQuestão 100
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
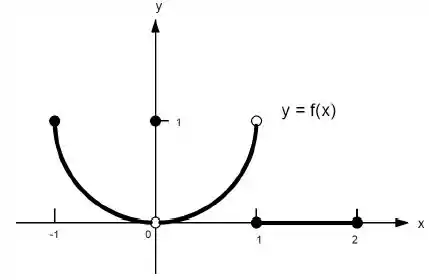
h)
Ver solução completaQuestão 101
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
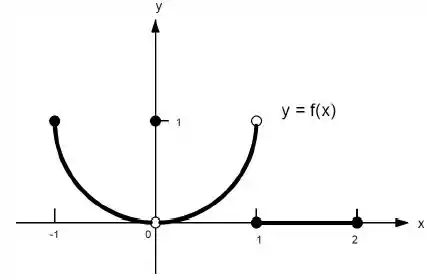
i)
Ver solução completaQuestão 102
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
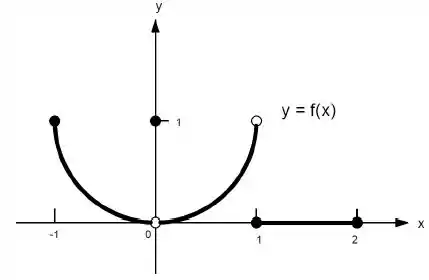
c)
Ver solução completaQuestão 103
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
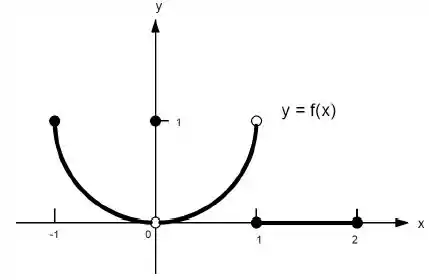
e) existe
Ver solução completaQuestão 104
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
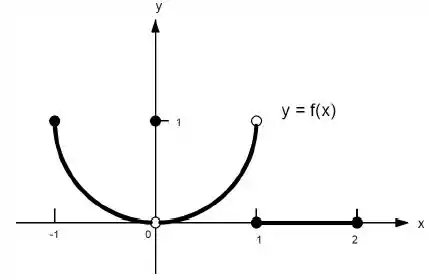
f)
Ver solução completaQuestão 105
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
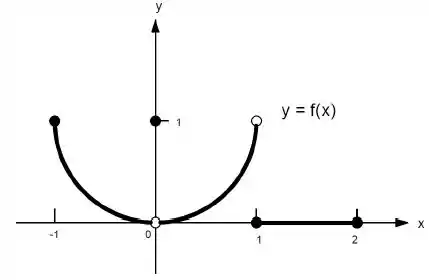
j)
Ver solução completaQuestão 110
Calcule os seguintes limites usando a regra de l’Hospital, indicando o tipo de indeterminação em cada caso:
a-
Ver solução completaQuestão 112
Sabe-se que e é definida em ℝ. Todas as afirmativas abaixo são falsas. Tente desenhar um contra - exemplo para cada uma delas.
- para
Questão 113
- Considere a fun ̧c ̃ao f cujo gr ́afico est ́a representado abaixo. Determine o que se pede.
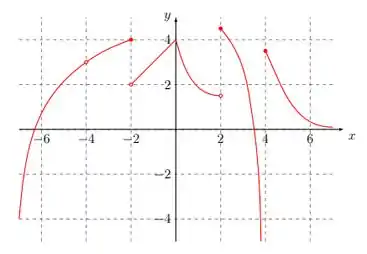
- Os limites e
- Os limites e
- Os limites e
- Os limites e
- Os limites e
- O que se pode dizer sobre a existência dos limites laterais nos pontos e ?
Questão 116
Calcule os seguintes limites, caso existir, justificando também se não existir
Ver solução completaQuestão 119
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 121
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
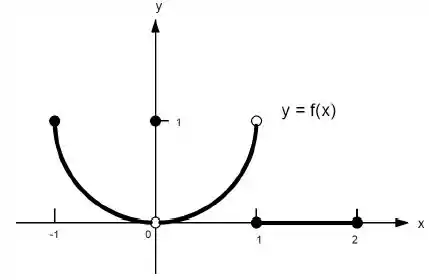
g)
Ver solução completaQuestão 122
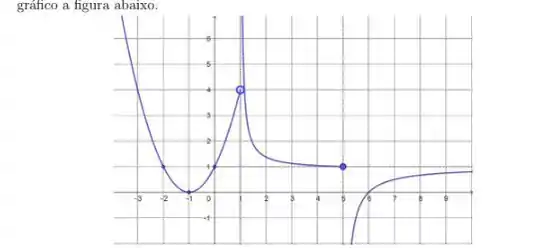
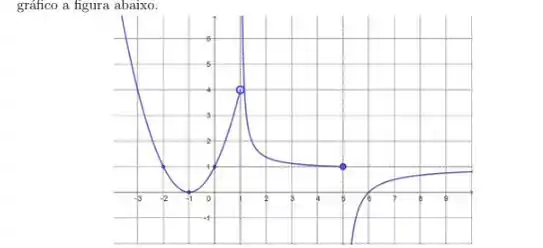
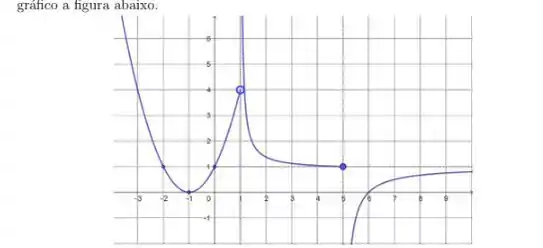
4. Seja
- Determine as quantidades a seguir, se existirem
- Esboce o gráfico de
Questão 128
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
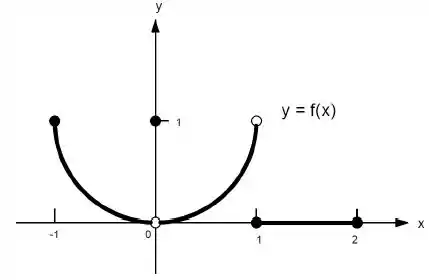
k) não existe
Ver solução completaQuestão 129
22. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
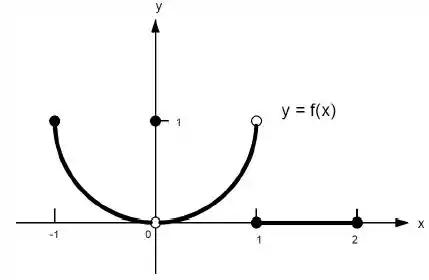
k)
Ver solução completaQuestão 130
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
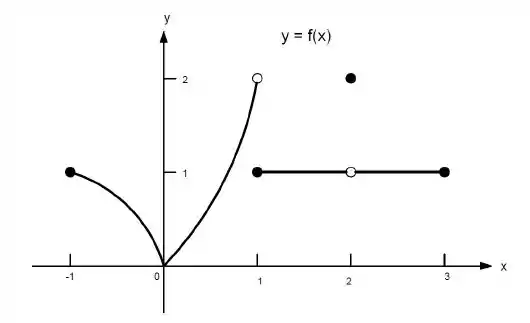
c)
Ver solução completaQuestão 131
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
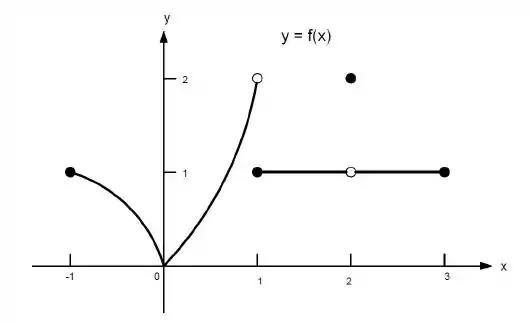
f)
Ver solução completaQuestão 132
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
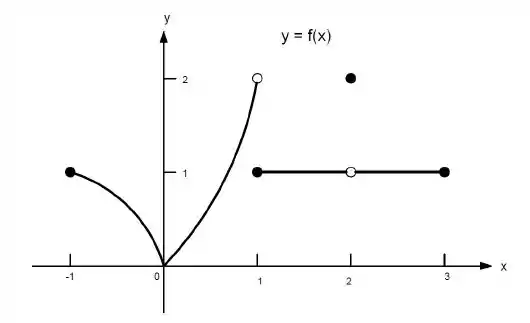
g) não existe
Ver solução completaQuestão 133
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
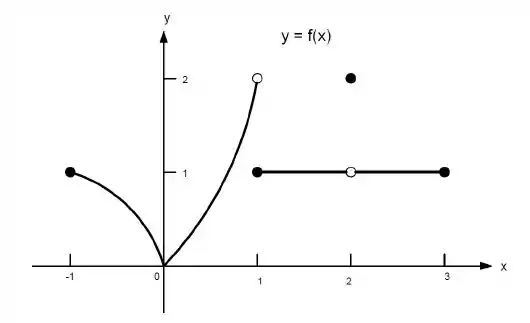
a)
Ver solução completaQuestão 134
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
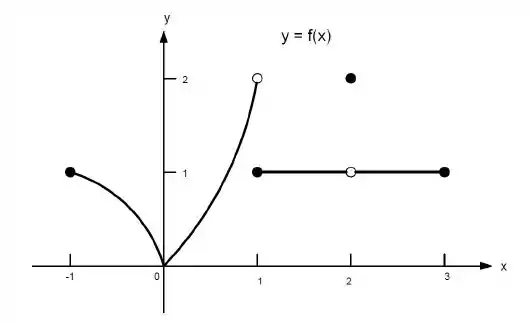
b) não existe
Ver solução completaQuestão 135
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
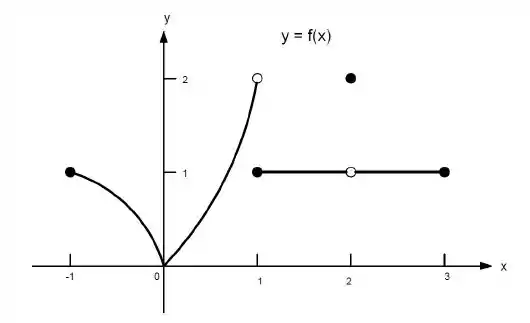
d)
Ver solução completaQuestão 136
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
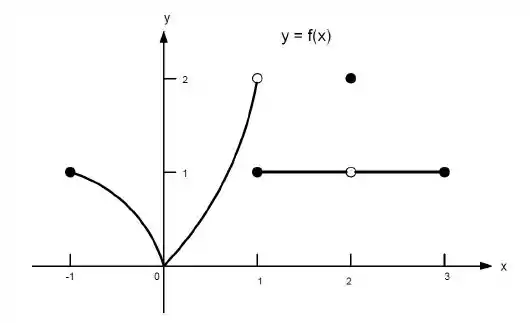
h) existe para qualquer no intervalo aberto .
Ver solução completaQuestão 137
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
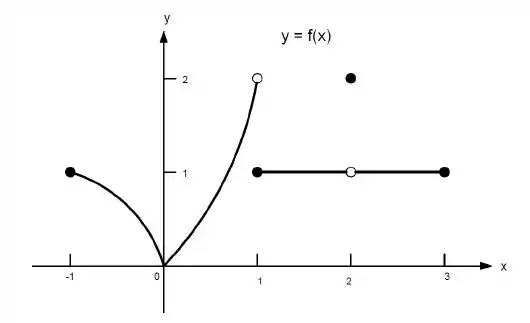
i) existe para qualquer no intervalo aberto .
Ver solução completaQuestão 138
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
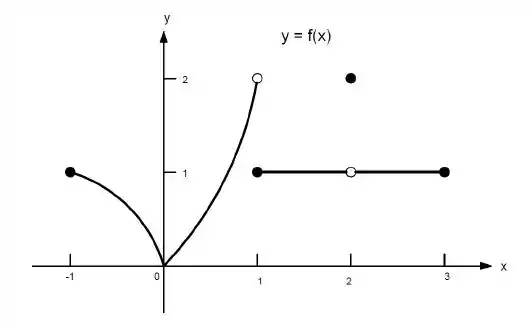
j)
Ver solução completaQuestão 139
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
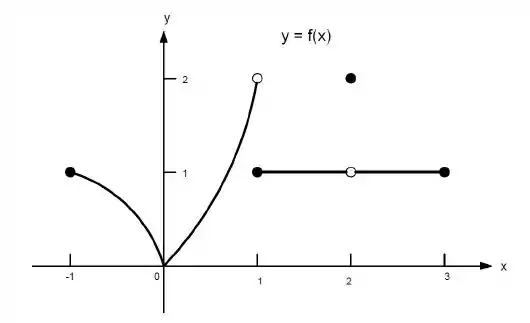
k) não existe.
Ver solução completaQuestão 140
24. c) Existe ? Em caso afirmativo, qual é? Em caso negativo, por que não?
Ver solução completaQuestão 142
25. c) Existe ? Em caso afirmativo, qual é? Em caso negativo, por que não?
Ver solução completaQuestão 144
Sabe-se quee é definida em . Todas as afirmativas abaixo são falsas. Tente desenhar um contra-exemplo para cada uma delas.
(a) para
(b)
(c) é positivo
Ver solução completaQuestão 149
A figura abaixo ilustra um corpo de massa pendurado no teto de um trem bala por
um fio inextensível de comprimento . Quando o trem possui aceleração, o pêndulo
se encontra inclinado, fazendo um ângulo com a vertical. Pode-se provar que, se é
a aceleração da gravidade local, então . Como temos que , onde a função é a função inversa da
tangente. Supondo que , resolva os itens seguintes.
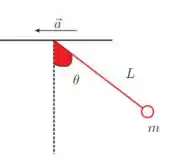
(a) Sabendo que , encontre
e
(b) Se a aceleração do trem tomar valores cada vez maiores, o ângulo se aproxima de que valor? E se , então tende para algum número?
(c) Faça um esboço dos gráficos de , com suas
assíntotas.
Ver solução completaQuestão 150
Para cada , o número positivo pode ser caracterizado como área da região
limitada pelo eixo , pelas retas verticais e pelo gráfico da função
. Por exemplo, o número é a área da região compreendida entre o gráfico
da função e as retas . Na figura foram destacados ainda três
retângulos de base unitária cujas alturas são.
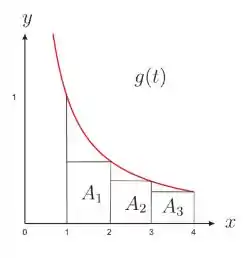
(a) Determine as areas dos retângulos indicados,
e faça sua soma.
(b) Usando o resultado anterior, justifique a desigualdade
.
(c) Dada uma constante arbitrariamente grande,
mostre que se ,então .
Conclua daí que: .
(d) Sabendo que para todo tem-se
investigue a existência de .
(e) Lembre que e calcule . Esboce o gráfico das funções
Ver solução completaQuestão 152
Quais os movimentos que devemos fazer no gráfico de uma função para obtermos o gráfico da inversa de ?
- Deslocar o gráfico de horizontalmente de unidades para a direita
- Deslocar o gráfico de horizontalmente de 2 unidades para a direita e fazer uma reflexão em torno do eixo
- Fazer uma reflexão em torno do eixo e deslocar o gráfico horizontalmente de unidades para a direita
- Deslocar o gráfico de verticalmente de unidades para cima e fazer uma reflexão em torno do eixo
- Fazer uma reflexão em torno do eixo e deslocar o gráfico de verticalmente de unidades para baixo
Questão 153
Dadas as funções:
E
(iii) Dê a expressão da função e verifique se existe .
Ver solução completaQuestão 155
Se para todo e , verifique se as afirmativas abaixo são verdadeiras ou falsas. Caso seja verdadeira, apresente uma justificativa. Caso seja falsa, apresente um contra-exemplo.
- não existe.
Questão 156
Se para todo e , verifique se as afirmativas abaixo são verdadeiras ou falsas. Caso seja verdadeira, apresente uma justificativa. Caso seja falsa, apresente um contra-exemplo.
- Se existir, é positivo.
Questão 157
Se para todo e , verifique se as afirmativas abaixo são verdadeiras ou falsas. Caso seja verdadeira, apresente uma justificativa. Caso seja falsa, apresente um contra-exemplo.
Questão 158
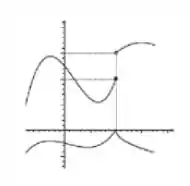
4) Os gráficos de e são dados. Ache os limites laterais de no pondo indicado.
e , ambas no ponto
Questão 159
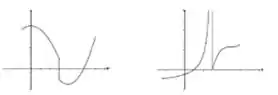
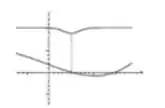
2) Os gráficos de e são dados. Ache os limites laterais de no pondo indicado.
, no ponto
Questão 160
3) Os gráficos de e são dados. Ache os limites laterais de no pondo indicado.
, no ponto
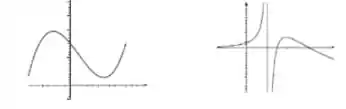
Questão 161
1) Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
, no ponto
Questão 163
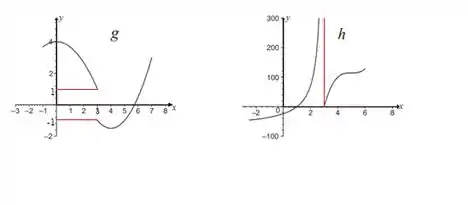
23. Quais afirmações a seguir sobre a função representadas no gráfico são verdadeiras e quais são falsas?
e)
Ver solução completaQuestão 165
Analise a continuidade da função:
- É contínua nos dois pontos
- É contínua em e descontínua em
- É contínua em e descontínua em
- É descontínua nos dois pontos
Questão 166
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(d)
Ver solução completaQuestão 169
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(a)
Ver solução completaQuestão 174
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
Questão 175
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado.
E
Ambas no ponto .
Questão 176
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 179
1. Suponha para todo e . Decida sobre a veracidade de cada uma das afirmações abaixo, justificando caso ela seja verdadeira ou apresentando um contraexemplo caso seja falsa.
b)
Ver solução completaQuestão 181
1. Suponha para todo e . Decida sobre a veracidade de cada uma das afirmações abaixo, justificando caso ela seja verdadeira ou apresentando um contraexemplo caso seja falsa.
a) não existe
Ver solução completaQuestão 182
1. Suponha para todo e . Decida sobre a veracidade de cada uma das afirmações abaixo, justificando caso ela seja verdadeira ou apresentando um contraexemplo caso seja falsa.
c) Se existir, é positivo.
Ver solução completaQuestão 183
2b) Calcule os limites abaixo ou prove que não existe (sem usar a Regra de L'Hospital).
Ver solução completaQuestão 184
C3. Esboce o gráfico de uma função que satisfaça todas as seguintes condições: , , e .
Ver solução completaQuestão 185
Os gráficos de e são dados. Ache os limites laterais de no ponto indicado
e
o
Ambas no ponto
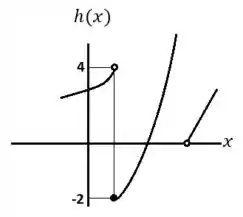
Questão 186
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(d)
Ver solução completaQuestão 187
Avalie os limites abaixo e encontre o correspondente valor caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(a)
Ver solução completaQuestão 188
Avalie os limites abaixo e encontre o correspondente valor caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(d)
Ver solução completaQuestão 189
Avalie os limites abaixo e encontre o correspondente valor caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(c)
Ver solução completaQuestão 190
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(b)
Ver solução completaQuestão 191
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(a)
Ver solução completaQuestão 192
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(d)
Ver solução completaQuestão 193
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(a)
Ver solução completaQuestão 194
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(b)
Ver solução completaQuestão 195
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(b)
Ver solução completaQuestão 196
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(a)
Ver solução completaQuestão 197
1. Suponha f(x) > 0 para todo x ≠ 2 e f(2) = −3. Decida sobre a veracidade de cada uma das afirmações abaixo, justificando caso ela seja verdadeira ou apresentando um contraexemplo caso seja falsa.
c) Se existir, é positivo.
Ver solução completaQuestão 198
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(a)
Ver solução completaQuestão 199
1. Suponha f(x) > 0 para todo x ≠ 2 e f(2) = −3. Decida sobre a veracidade de cada uma das afirmações abaixo, justificando caso ela seja verdadeira ou apresentando um contraexemplo caso seja falsa.
c) Se existir, é positivo.
Ver solução completaQuestão 200
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(b)
Ver solução completaQuestão 201
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(a)
Ver solução completaQuestão 202
Avalie os limites abaixo e encontre o valor correspondente, caso exista.
(b)
Ver solução completaQuestão 203
1 – Escolha e calcule dos seguintes limites (não utilizar o teorema de ):
b)
Ver solução completaQuestão 204
1 – Escolha e calcule dos seguintes limites (não utilizar o teorema de ):
a)
Ver solução completaQuestão 206
1 – Escolha e calcule dos seguintes limites (não utilizar o teorema de ):
d)
Ver solução completaQuestão 207
1 – Escolha e calcule dos seguintes limites (não utilizar o teorema de ):
c)
lembrando que
Ver solução completaQuestão 208
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(c)
Ver solução completaQuestão 210
Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.
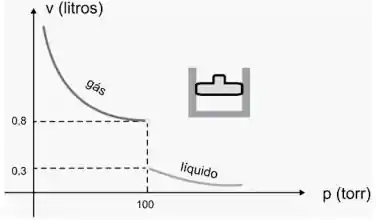
(a)
Ver solução completaQuestão 211
Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.
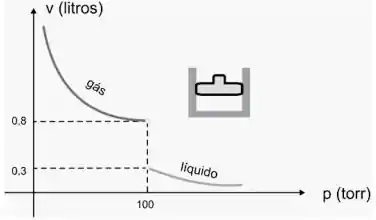
(b)
Ver solução completaQuestão 212
Um gás (tal como vapor d’água ou oxigênio) é mantido à temperatura constante no pistão. A medida que o gás é comprimido, o volume (V ) decresce até que atinja uma certa pressão (p) crítica. Além dessa pressão, o gás assume forma líquida. Use o gráfico da figura a seguir para resolver e interpretar.
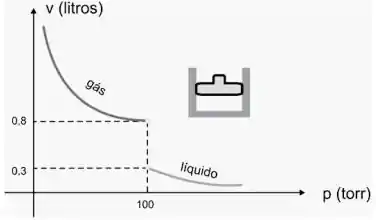
(c) Existe . Por que?
Ver solução completaQuestão 213
2.1) Determine o limite, se existir, ou mostre que o limite não existe exibindo caminhos que levam a limites diferentes ou para os quais o limite não existe
a)
b)
c)
d)
e) Dica: considere os caminhos
Ver solução completaQuestão 214
- a) Determine as assíntotas horizontais e verticais, caso existam, da seguinte função:
Ver solução completaQuestão 215
2.1) Determine o limite, se existir, ou mostre que o limite não existe exibindo caminhos que levam a limites diferentes ou para os quais o limite não existe
a)
b)
c)
d)
e) Dica: considere os caminhos
Ver solução completaQuestão 216
2.1) Determine o limite, se existir, ou mostre que o limite não existe exibindo caminhos que levam a limites diferentes ou para os quais o limite não existe
a)
b)
c)
d)
e) Dica: considere os caminhos
Ver solução completaQuestão 222
Certas fórmulas que representam quantidades físicas podem conduzir a limites que envolvam infinito. Claramente, uma grandeza física não pode tender para infinito, mas uma análise de uma situação hipotética em que tal fato pudesse ocorrer, pode sugerir usos para outras quantidades relacionadas. Vejamos os seguintes exemplos.
A lei de Ohm na teoria da eletricidade afirma que , onde é a resistência (em ohms) de um condutor, é a diferença de potencial (em volts) através do condutor e é a corrente (em ampères) que passa pelo condutor. A resistência de certas ligas tende para zero quando a temperatura se aproxima do zero absoluto (aproximadamente ), e a liga se torna um supercondutor de eletricidade. Se a voltagem é fixa, então, para esse
supercondutor,
isto é, a corrente aumenta sem limite. Os supercondutores permitem que grandes correntes sejam usadas em usinas geradoras ou motores. Eles têm também aplicações no transporte terrestre a alta velocidade, no qual o forte campo magnético produzido por magnetos supercondutores permitem que os trens levitem, não havendo essencialmente fricção entre as rodas e os trilhos. Possivelmente a utilização mais importante para os supercondutores está nos circuitos para computadores, porque esses circuitos produzem pouquíssimo calor.
Ver solução completaQuestão 223
3. Calcule os limites abaixo ou prove que não existe (sem usar a Regra e L’Hospital). Justifique suas passagens com detalhes!
b.
Ver solução completaQuestão 227
10. Se , deve existir? Em caso afirmativo, deve ser ? Podemos concluir algo sobre ? Explique.
Ver solução completaQuestão 228
9. Suponhamos que a função seja definida para todo em . O que pode ser dito sobre a existência de . Justifique sua resposta.
Ver solução completaQuestão 229
Estude se as funções abaixo tem limite nos pontos indicados.
, ponto .
Ver solução completaQuestão 230
Estude se as funções abaixo tem limite nos pontos indicados.
, ponto .
Ver solução completaQuestão 231
27. Explique o que significa dizer que e .
Nesta situação, é possível que exista? Explique.
Ver solução completaQuestão 234
Considere a função
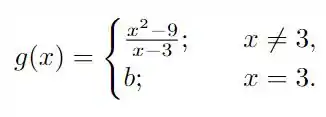
esta função tem limite em ? Qual deve ser o valor de para que a função seja contínua?
Ver solução completaQuestão 239
Seja . Mostre que essa sequência é crescente e limitada (por exemplo, pelo ).
Ver solução completaQuestão 243
3. Uma função satisfaz as seguintes propriedades:
- e
- é estritamente crescente em e
- é uma função par
b. Determine os seguintes valores: e
Ver solução completaQuestão 244
Encontre o ponto sobre a curva (definida para ) que está mais próximo da origem.
Ver solução completaQuestão 245
- b) Determine as assíntotas horizontais e verticais, caso existam, da seguinte função:
Ver solução completaQuestão 246
Para cada um dos itens a seguir, mostre que o limite existe ou não. Determine o limite caso exista.
Ver solução completaQuestão 248
Avalie os limites abaixo e encontre o correspondente valor caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(b)
Ver solução completaQuestão 250
Discuta de modo argumentativo a existência ou inexistência de cada um dos limites abaixo, determinando-o quando este existir:
Ver solução completaQuestão 251
Seja a função
Um aluno calculou , percebeu que esses números têm sinais
contrários e concluiu que deve existir tal que . Você
concorda com ele? Justifique.
Ver solução completaQuestão 252
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(c)
Ver solução completaQuestão 253
Considere a função
Determine se existe tal que é contínua. Caso exista, encontre o valor de . Em qualquer caso, justifique sua resposta.
Ver solução completaQuestão 270
Considere uma função e um número real de modo que . Suponha que exista um número tal que , para todo .
Prove que
Ver solução completaQuestão 271
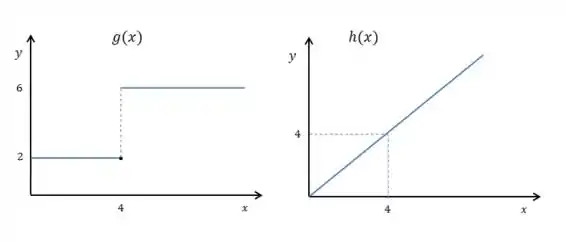
Suponha que ao se consumir de água por mês, o valor mensal a ser pago seja reais. Quando é menor ou igual a , paga-se , quando é maior, paga-se , onde é uma quantidade.
- Considerando o contexto da questão, determine a expressão da função e explique por que ela possui comportamento estranho caso a constante seja zero
- Usando a definição de continuidade, determine o valor de para que a função seja contínua em
Questão 277
Considere a função
- Esboce o gráfico de .
- Calcule e .
- Existe o ? Justifique.
Questão 282
Discuta de modo argumentativo a existência ou inexistência de cada um dos limites abaixo, determinando-o quando este existir:
Ver solução completaQuestão 284
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 292
2. Considere a função
- Determine e todos os limites de no ponto .
- Determine e todos os limites de no ponto .
- Determine e todos os limites de no ponto .
- Determine e todos os limites de no ponto .
- Determine e todos os limites de no ponto .
- Determine e todos os limites de no ponto .
Questão 294
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(b)
Ver solução completaQuestão 297
2.1) Determine o limite, se existir, ou mostre que o limite não existe exibindo caminhos que levam a limites diferentes ou para os quais o limite não existe
a)
b)
c)
d)
e) Dica: considere os caminhos
Ver solução completaQuestão 298
Calcule os seguintes limites usando a regra de l’Hospital, indicando o tipo de indeterminação em cada caso:
b-
Ver solução completaQuestão 301
2.1) Determine o limite, se existir, ou mostre que o limite não existe exibindo caminhos que levam a limites diferentes ou para os quais o limite não existe
a)
b)
c)
d)
e) Dica: considere os caminhos
Ver solução completaQuestão 302
2 – Para que a função abaixo seja continua em ela deve satisfazer três condições ao mesmo tempo. Diga quais são essas condições e encontre o valor de que as satisfaça. (não utilizar o teorema de ).
Ver solução completaQuestão 305
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 306
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 309
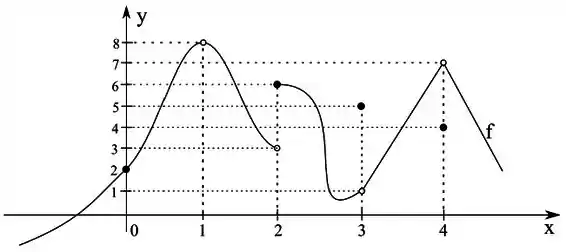
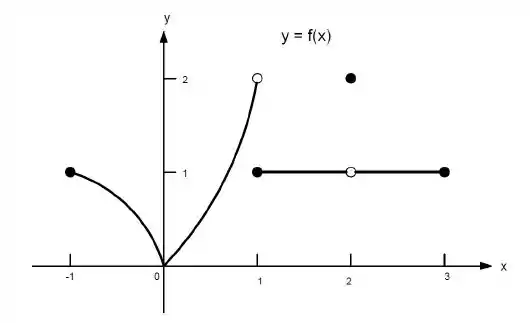
C1. Para a função cujo gráfico é mostrado a seguir, determine o valor de cada quantidade, se ela existir.
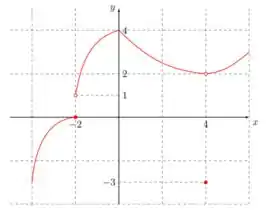
(a) . (b) . (c) . (d) .
(e) . (f) . (g) . (h) .
Ver solução completaQuestão 310
Considere uma função e um número real de modo que . Suponha que exista um número tal que , para todo .
Prove que
- Use o limite em para calcular:
Questão 311
Considere uma função e um número real de modo que . Suponha que exista um número tal que , para todo .
Prove que
- Use o limite em para calcular:
Questão 316
Considere os limites abaixo e determine-os caso exista. É importante lembrar que para todo
Ver solução completaQuestão 318
Calcule os seguintes limites (Não é permitido o uso da regra de l’Hôspital):
a)
Ver solução completaQuestão 326
4. Considere a função onde estiver definida. É incorreto afirmar que:
a)
b)
c)
d)
e)
Ver solução completaQuestão 327
9. Calcule o limite, caso exista, os especifique porque não existe. Não é permitido usar derivada. Lembre-se de justificar sua resposta.
a)
b)
Ver solução completaQuestão 340
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
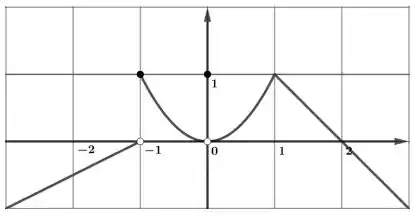
b)
Ver solução completaQuestão 341
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
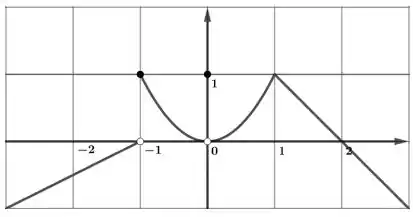
f)
Ver solução completaQuestão 343
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
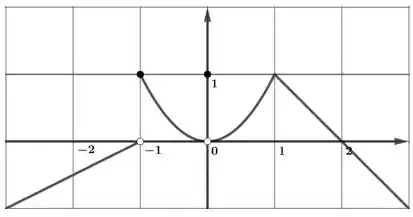
a)
Ver solução completaQuestão 344
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
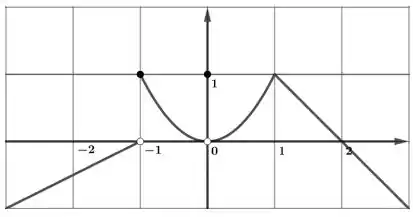
c)
Ver solução completaQuestão 345
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 346
Calcule, caso exista, cada um dos limites abaixo. Se não existir, justifique.
Questão 349
Seja dada por
a) Calcule e
b) Determine os valores de para que a equação admita exatamente duas soluções reais distintas.
Ver solução completaQuestão 352
3. Seja , uma função contínua em todo seu domínio ou . Sobre se sabe:
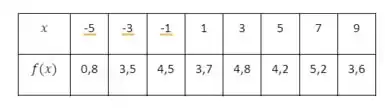
b) Se, além da tabela acima, também souber que
como isso afeta, se é que afeta, suas conclusões sobre o número garantido de soluções da equação ?
Ver solução completaQuestão 361
Considere os limites abaixo e determine-os caso exista. É importante lembrar que para todo
Ver solução completaQuestão 366
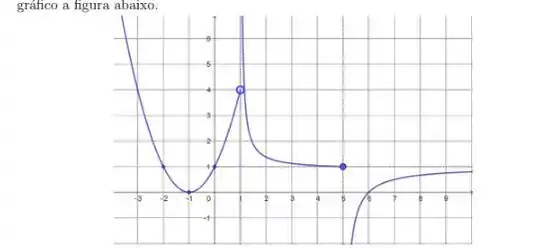
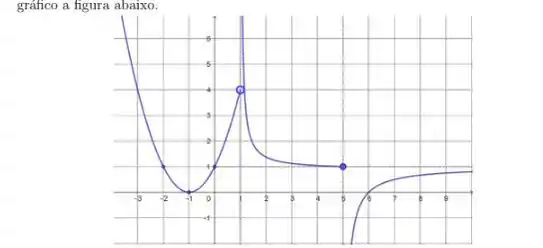
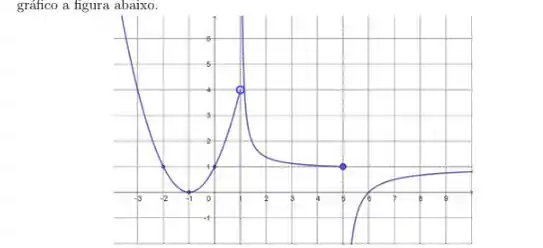
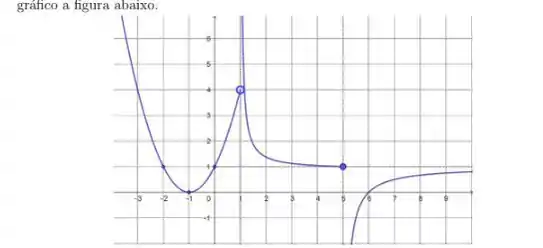
1. Uma função com domínio tem como gráfico a figura abaixo.
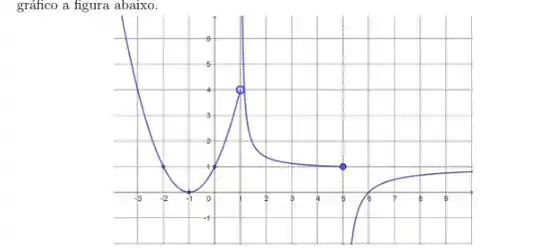
a) Estude os limites laterais e diga o que pode concluir sobre
Ver solução completaQuestão 368
Em cada item, diga se as propriedades permitem que o limite possa ser calculado apenas substituindo x. Se a resposta for sim, calcule o limite. Use as propriedades vistas na vídeo aula.
Ver solução completaQuestão 369
5. Encontre, quando existir, o limite. Caso não exista, explique por quê.
Questão 372
Avalie os limites abaixo e encontre o valor correspondente caso exista (sem usar a regra de L’Hospital). Justifique suas respostas.
(b)
Ver solução completaQuestão 376
7. Seja para .
d) Calcule o limite, quando se aproxima de 2, da taxa média de variação de com relação a no intervalo de a . Você precisará fazer alguns cálculos algébricos antes de substituir .
Ver solução completaQuestão 378
Para a função cujo gráfico é dado, diga o valor de cada quantidade, se ela existir. Se não existir, explique porquê.
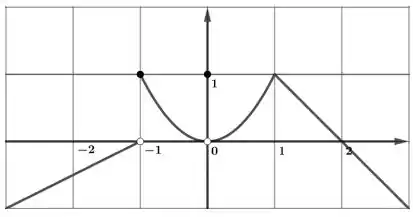
d)
Ver solução completa