Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 8

Use o roteiro desta seção para esboçar a curva:

y = 4 - x 2 5

Passo 1

Falaii galerinha do Responde ai, tudo belezinha?

A questão pede para esboçar a curva da função

y = 4 - x 2 5

Esboçar a curva significa desenhar o gráfico da função para entender melhor seu comportamento.

Para esboçar o gráfico da função, podemos seguir alguns passos fundamentais:

1. Encontrar o domínio da função.

2. Determinar os pontos de interceptação com os eixos.

3. Analisar o comportamento da função em termos de crescimento e decrescimento.

4. Identificar pontos críticos e inflexões.

5. Observar o comportamento da função nos limites extremos (quando x tende ao infinito ou menos infinito).

6. Esboçar o gráfico com base nessas informações.

Passo 2

Domínio da Função

A função

  y   =   4   –   x 2 5

é definida para todos os valores de (   x   ) onde (   4   –   x 2 ) é maior ou igual a zero, já que não podemos elevar um número negativo a uma potência fracionária no campo dos números reais.

4 - x 2 ≥ 0

x 2 ≤ 4

- 2 ≤ x ≤ 2

Então, o domínio da função é - 2 ≤ x ≤ 2

Interceptação com os Eixos

Para encontrar a interceptação com o eixo (   y   ) , fazemos (   x   =   0   ) :

y 0 =   4   -   0 2 5 =   4 5 =   1024

A função intercepta o eixo (   y   ) no ponto   ( 0 ,   1024 ) .

Para encontrar a interceptação com o eixo (   x   ) , fazemos (   y   =   0   ) :

4   -   x 2 5 =   0  

4   -   x 2 =   0  

  x 2 =   4  

  x   =   ± 2

A função intercepta o eixo (   x   ) nos pontos ( - 2 ,   0 )     e   ( 2 ,   0 )   .

Passo 3

Crescimento e Decrescimento

Para analisar o comportamento da função, calculamos a primeira derivada:

y   =   4   -   x 2 5

y ' =   5 4   -   x 2 4 ⋅ - 2 x

=   - 10 x 4   -   x 2 4

Analisamos o sinal da derivada para determinar onde a função cresce ou decresce. Observamos que (   y ' =   0   ) quando

(   x   =   0   )   o u   (   x   =   ± 2   )

Para

(   - 2   <   x   <   0   ) ,   (   y ' >   0   )   e n t ã o   a   f u n ç ã o   é   c r e s c e n t e .

Para

(   0   <   x   <   2   ) ,   (   y ' <   0   )   e n t ã o   a   f u n ç ã o   é   d e c r e s c e n t e .

Nos extremos

(   x   =   - 2   )   e   (   x   =   2   )

A derivada é zero, indicando possíveis pontos de máximo ou mínimo.

Pontos Críticos e Inflexões

Para encontrar pontos de inflexão, calculamos a segunda derivada:

y ' =   - 10 x 4   -   x 2 4

y ' ' =   - 10     4   -   x 2 4 +   x   ⋅ 4 4   -   x 2 3 ⋅ - 2 x

=   - 10     4   -   x 2 4 -   8 x 2 4   -   x 2 3

Passo 4

Simplificar e analisar os pontos onde a segunda derivada muda de sinal dá os pontos de inflexão.

Limites Extremos

Como o domínio é finito, analisamos x nos limites do domínio:

Para

(   x   =   ± 2   ) ,   (   y   =   0   )

Analise Gráfica:

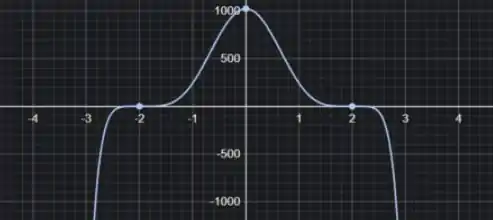
- O gráfico mostra que a função tem simetria em relação ao eixo (   y   ) .

- A função atinge seu valor máximo em (   x   =   0   )   c o m   (   y   =   1024   ) .

- Nos pontos (   x   =   ±   2   ) , a função toca o eixo   (   x   )   c o m   (   y   =   0   ) .

- A função é crescente de (   x   =   - 2   ) até (   x   =   0   ) e decrescente de ( x = 0 )   a t é   ( x = 2 ) .

“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”

Resposta

Vide a explicação.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Investigue a família de curvas dadas por f x = x e - c x , em que c é um número real. Comece calculando os limites quando x → ± ∞ . Identifique qualquer valor intermediário de c onde mude a forma bási
Descreva a mudança no gráfico def à medida que c varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos d
Descreva a mudança no gráfico def à medida que c varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos d
Use o roteiro desta seção para esboçar a curva: y = 2 x - tan ⁡ x ,- π 2xπ 2
Descreva a mudança no gráfico def à medida que c varia. Faça o gráfico de vários membros da família para ilustrar as tendências que você descobriu. Em particular, você deve investigar como os pontos d