Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.4 - Ex. 25

Esboce a região definida pelas desigualdades - 1 <= r <= 2 e - pi // 2 <= theta <= pi // 2 .

Passo 1

Oi galerinha, vem comigo!

Quando utilizamos coordenadas polares e cartesianas em um plano, posicionamos as duas origens juntas e tomamos o raio polar inicial como o eixo x positivo. O raio theta = pi // 2 , r > 0 , torna-se o eixo y positivo. Os dois sistemas de coordenadas estão relacionados.

As seguintes equações determinam unicamente as coordenadas cartesianas x e y , dadas as coordenadas polares r e theta :

Sabemos que a circunferência para - pi // 2 <= theta <= pi // 2 , é dado por:

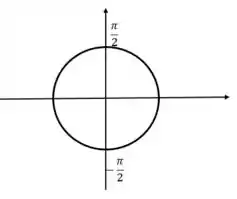
Passo 2

Para r = - 1 :

  • theta = - pi // 2 :

    • x = - 1 cos (- (pi)/(2)) = 0

    y = - 1 sen (- (pi)/(2)) = 1

  • theta = pi // 2 :

    • x = - 1 cos ((pi)/(2)) = 0

    y = - 1 sen ((pi)/(2)) = - 1

    Então, temos:

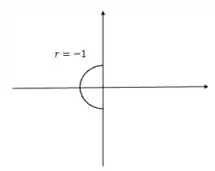
    Passo 3

    Para r = 2 :

  • theta = - pi // 2 :

    • x = 2 cos (- (pi)/(2)) = 0

    y = 2 sen (- (pi)/(2)) = - 2

  • theta = pi // 2 :

x = 2 cos ((pi)/(2)) = 0

y = 2 sen ((pi)/(2)) = 2

Temos:

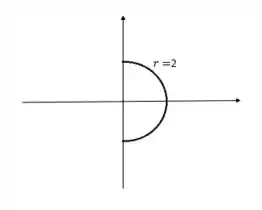
Passo 3

Então nossa região fica da seguinte forma:

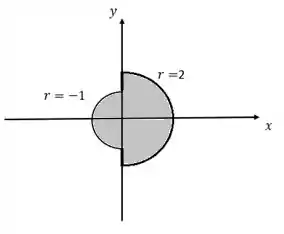
Espero ter conseguido te ajudar. Tchau pessoal.

Resposta

Resposta no Passo 4.

Exercícios de Livros Relacionados

Demarque o seguinte ponto no sistema de coordenadas polares. P 3 - 4 , π 4
Encontrar um par de coordenadas polares do seguinte ponto: - 1,1
Demarque o seguinte ponto no sistema de coordenadas polares. P 4 - 4 , - π 4
Encontrar as coordenadas cartesianas do seguinte ponto dado em coordenadas polares. 1 , 0
Demarcar o seguinte ponto no sistema de coordenadas polares e encontrar suas coordenadas cartesianas. - 3 , π 3