Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 9.Exercícios - Ex. 208c

Estude a variação das seguintes funções reais: c) h (x) = cos^4 x + s e n^4 x

Passo 1

Nosso primeiro passo será reescrever a expressão da nossa função em algo mais fácil de se estudar. Neste caso, vamos usar a técnica de completar quadrados da seguinte forma:

(cos^2 x + s e n^2 x)^2 = cos^4 x + 2 * cos^2 x * s e n^2 x + s e n^4 x

Podemos perceber que a expressão acima é quase igual à da nossa função h ( x ) mas para ficar igual, nós precisamos retirar aquela parcela do meio, ou seja, podemos escrever a função como: h (x) = (cos^2 x + s e n^2 x)^2 - 2 * cos^2 x * s e n^2 x

Usando a relação fundamental da trigonometria, podemos substituir (cos^2 x + s e n^2 x)^2 = 1 , ficando com: h (x) = 1 - 2 * cos^2 x * s e n^2 x

Passo 2

Agora vamos focar na segunda parcela da função. Vale relembrar a fórmula:

s e n 2 a = 2 * s e n a * cos a

s e n^2 2 a = (2 * s e n a * cos a)^2

s e n^2 2 a = 4 * s e n^2 a * cos^2 a

(s e n^2 2 a)/(2) = 2 * s e n^2 a * cos^2 a

Usando um pouco de percepção, conseguimos substituir nossa função por:

h (x) = 1 - 2 * cos^2 x * s e n^2 x = 1 - (s e n^2 2 x)/(2)

h (x) = 1 - (s e n^2 2 x)/(2)

Passo 3

Para simplificar ainda mais a nossa função, podemos pensar na fórmula:

cos 2 a = 1 - 2 * s e n^2 a

2 * s e n^2 a = 1 - cos 2 a

s e n^2 a = (1 - cos 2 a)/(2)

Se atentando ao fato de que, na função, temos s e n^2 2 x , então vamos substituir por:

h (x) = 1 - ((1 - cos 4 x)/(2))/(2) = 1 - (1 - cos 4 x)/(4) Fazendo o mmc afim de resumir a expressão, ficaremos com: h (x) = (4 - (1 - cos 4 x))/(4) = (3 + cos 4 x)/(4) = (3)/(4) + (cos 4 x)/(4)

Passo 4

Agora podemos estudar nossa função h (x) = (3)/(4) + (cos 4 x)/(4) de forma mais eficiente, para isso vamos utilizar uma tabela: 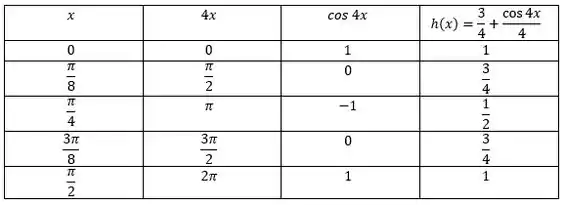I m h = 1 2 , 1

I m (h) = [(1)/(2) , 1]

D (h) = R

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

Encontre o domínio de cada função:(a) g (t) = sen ( e^(- t) ) (b) g (t) = sqrt(1 - 2^t)
f : R - R d a d a p o r f (x) = - 1 + s e n 2 x
f : R - R d a d a p o r f (x) = 1 + 2 s e n ((x)/(2) - (pi)/(6))
Estude a variação das seguintes funções reais: a) f (x) = cos^4 x - s e n^4 x