Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 2.1 - Ex. 8j
Estude a variação de sinal de .
Passo 1
Nesse caso, temos um quoticente de dois polinômios.
Vamos primeiro avaliar o denominador que deve ser diferente de zero, já que não existe divisão por zero:
Pela inequação vemos que o quadado de um número qualquer deve ser diferente de um número negativo (), assim podemos escolher qualquer número real para visto que o quadrado de qualquer número real é sempre positivo, ou seja, não possui raizes reais e é sempre positivo.
Passo 2
Assim, a raiz da função é:
Passo 3
Assim, podemos construir uma tabela analisando o sinal de cada termo da função e a respectiva divisão dos termos que gera :
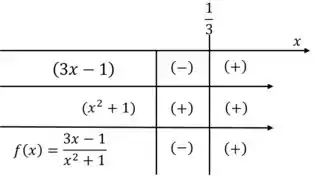
Assim, temos que:
para
para
Resposta
para
para
Exercícios de Livros Relacionados
21. Encontre o domínio de y = x + 3 4 - x 2 - 9
24. Faça os gráficos das equações a seguir e explique por que eles não são gráficos de funções de x .a. x + y = 1
23. Faça os gráficos das equações a seguir e explique por que eles não são gráficos de funções de x .a. y = x
Encontre uma fórmula para cada função representada por meio de gráficos nos Exercícios 29-32.29. b.
24. Faça os gráficos das equações a seguir e explique por que eles não são gráficos de funções de x .a. x + y = 1