Nos Exercícios 1-12, calcule a integral iterada.
Passo 1
Fala galerinha tranquilidade, seguinte nesses exercícios nós teremos que integrar cada váriavel mantendo a outra constante, como se fosse uma derivada parcial, isso porque vamos utlizar o teorema de Fubini, que diz que podemos calcular um volume por meio de uma integral dupla em relação ao plano xy, a deinição diz o seguinte:
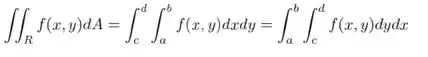
Desde que a função seja contínua entre os limites de ingração do retângulo.
Passo 2
Com isso podemos calcular as integrais usando o método mais conveniente, é imporante que se faço o cálculo das funções mais internas para as mais externas. Temos então o seguinte:
Vamos resolver de dentro para fora:
Repare que o termo com se torna constante, já que estamos integrando em !
Com isso, ficamos com:
Agora essa integral é tranquila de resolver. Ficamos com:
Avaliando nos limites de integração, temos:
Passo 3
Nossa integral se torna, então:
Resolvendo essa integral, podemos tirar os termos que não dependem de !
Dessa forma, temos:
Podemos fazer uma rápida substituição, na forma:
Os novos limites serão:
E
Com isso, teremos:
Ou seja:
Essa integral, de novo, é tranquila de resolver. Temos então:
Simplificando a expressão:
Com isso, nossa expressão inicial que queríamos resolver, se torna: