Nos exercícios a , temos uma comporta de uma represa, colocada verticalmente, com a forma indicada.

Calcular a força total contra a comporta

29.Um triângulo isósceles com de largura no topo e de altura; nível d’ água: coincide com o topo da comporta.

Vamos desenhar o “gráfico” da comporta, e assim conseguiremos tirar as informações que estão nessa integral, com origem na origem do plano cartesiano.

.

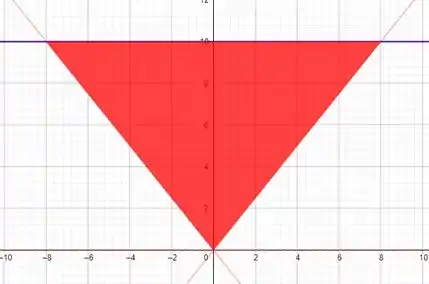
A comporta está em vermelho, é delimitada em baixo pelos pontos e, pois admitimos esse triangulo com origem na origem do plano cartesiano.

Em cima é delimitada pelos pontos e , pois o topo precisa medir e o triângulo tem altura de .

Então,

A comporta é delimitada à esquerda pela reta que passa pelos pontos e . A reta que passa por esses pontos é a e isolando o , temos :

À direita a comporta é delimitada pela reta, também, mas essa passa pelos pontos e A reta que passa por esses pontos é a só que precisamos de , então isolando o , temos: .

Agora, vamos isolar as nossas funções! É o passo mais fácil!

Para finalizar nossa análise, apenas temos que ver o nível da água, em azul. Ora, o nível de água é o mesmo da altura da comporta segundo o enunciado.

Substituindo tudo na integral e sabendo que o peso da água por metro cúbico é .

Focando só na integral, temos: