Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.2 - Ex. 19

Nos Exercícios 19-24, esboce a região de integração e calcule a integral.

∫ 0 π ∫ 0 x x sen ⁡ y d y   d x

Passo 1

Olá pessoal, primeiramente vamos esboçar a nossa região de integração, onde:

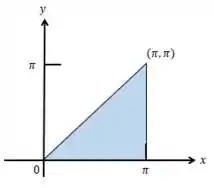
Do enunciado temos a seguinte integral:

∫ 0 π ∫ 0 x x sen ⁡ y d y   d x

Vamos, primeiro, derivar em função de y , e sabemos que:

∫ sen ⁡ u d u = - cos ⁡ u

Logo:

= ∫ 0 π x   ∙ - cos ⁡ y 0 x d x

= - ∫ 0 π x   ∙ cos ⁡ y 0 x d x

= - ∫ 0 π x   ∙ cos ⁡ x - cos ⁡ 0 d x

= - ∫ 0 π x   ∙ cos ⁡ x - 1 d x

= - ∫ 0 π x cos ⁡ x - x d x

Passo 2

Para integrarmos a parte x cos ⁡ x , precisamos fazer por partes, ou seja:

∫ f d g = f g - ∫ g d f

Então temos o seguinte f = x                   d g = cos ⁡ x , logo:

d f = d x g = sen ⁡ x

Então:

∫ x cos ⁡ x = x sen ⁡ x - ∫ sen ⁡ x d x

= x sen ⁡ x - - cos ⁡ x

= x sen ⁡ x + cos ⁡ x

Passo 3

Voltando para integral original:

= - ∫ 0 π x cos ⁡ x - x d x = - x sen ⁡ x + cos ⁡ x - x 2 2 0 π

= - x sen ⁡ x - cos ⁡ x + x 2 2 0 π

= - π sen ⁡ π - cos ⁡ π + π 2 2 - - 0 sen ⁡ 0 - cos ⁡ 0 + 0 2 2

= 0 - - 1 + π 2 2 - 0 - 1 + 0

= 1 + π 2 2 + 1

= π 2 2 + 2

Tchau galerinha, até mais!

Resposta

π 2 2 + 2

Exercícios de Livros Relacionados

Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 1 2 ∫ y y 2 d x d y
Nos Exercícios 19-24, esboce a região de integração e calcule a integral. ∫ 0 ln ⁡ 8 ∫ 0 ln ⁡ y e x + y d xd y
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = 0 , x = 0 , y = 1
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = 3 - 2 x , y = x e
Nos Exercícios 9-18, escreva a integral iterada de ∬ Rd A sobre a região descrita R utilizando (a) seções transversais verticais, (b) seções transversais horizontais.Limitada por y = e - x , y = 1 e x