Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.1 - Ex. 45
Faça um esboço do gráfico da função dada.
Passo 1
A questão pede para esboçarmos o gráfico da função . Para esboçarmos gráficos de funções trigonométricas inversas, uma dica muito importante é ver o comportamento da função trigonométrica correspondente.
Para isso, vamos inverter a relação :
Assim, é a função inversa de , isto é, , onde
Vamos esboçar primeiro o gráfico de :
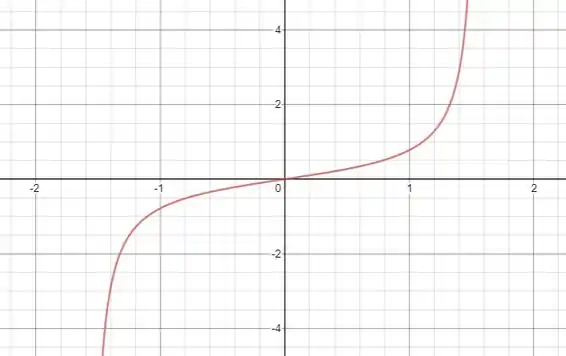
Para que tenha inversa ela deve ser injetora, por isso restringimos seu domínio para o intervalo . Sua imagem vai de até .
Passo 2
Como é o inverso de , seu domínio vai de até , porém sua imagem é restrita ao intervalo . Para traçar o gráfico de , basta lembrar que o gráfico de uma função e sua inversa são simétricos com relação a reta . Assim, o gráfico de será
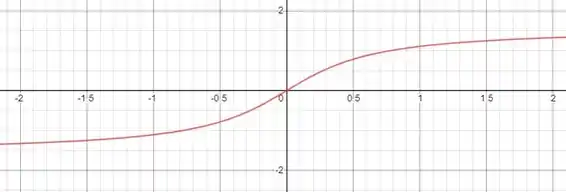
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
Enfocando conceitosEm cada parte, determine se a função f definida pela tabela é injetora
Verifique suas respostas para o Exercício 1 com um recurso gráfico computacional, determinando se os gráficos de f e g são reflexões um do outro em relação à reta y = x
Em (a)-(d), determine se f e g são funções inversas a )f x = 4 x , g x = 1 4 x b )f x = 3 x + 1 , g x = 3 x - 1 c )f x = x - 2 3 , g x = x 3 + 2 d )f x = x 4 , g x = x 4
Em cada parte, use o texto da reta horizontal para determinar se a função f é injetora: a )f x = 32 + x b )f x = x - 1 c )f x = x d )f x = x 3 e )f x = x 2 - 2 x + 2 f )f x = sen x
Encontre a fórmula para f - 1 x 11 )f x = 3 x 3 - 5