Exercícios de Funções Injetoras, Sobrejetoras, Bijetoras e Inversas - Lista de Exercícios Resolvida
Questão 1
Para as funções em representadas abaixo qual é injetora? E sobrejetora? E bijetora?
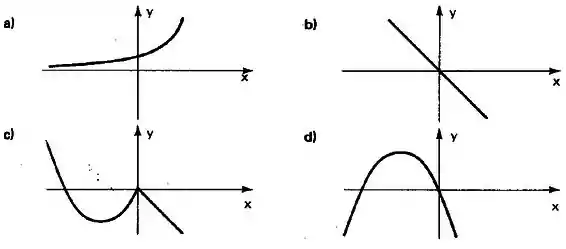
Questão 2
Determine o valor de em de modo que a função de em definida por seja SOBREJETORA.
Ver solução completaQuestão 14
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 15
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 16
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 17
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 18
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 19
Mostre que as funções definidas são bijetoras e determine a sua função inversa.
tal que
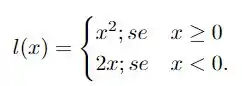
Questão 20
Todas as funções abaixo são injetoras (verifique!). Encontre a inversa dessas funções (assumindo contradomínio igual ao conjunto imagem).
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
Ver solução completaQuestão 21
Seja a função definida por
Considere .
(a) Mostre que a função (definida no domínio acima) é inversível.
(b) Determine
Dica: Não é necessário determinar a expressão da função inversa de
(c) Determine a equação da reta tangente ao gráfico de em
Ver solução completaQuestão 22
- Seja um número real e considere a função dada por
O maior valor de para o qual é uma função injetiva é
- ;
- ;
- ;
- .
Questão 23
Determine a inversa da função
Identifique o domínio e imagem da inversa de , denotada por
Ver solução completaQuestão 26
Nos itens a seguir são representados, em diagrama de flechas ou no plano cartesiano, os gráficos de algumas funções. Classifique-as em injetora, sobrejetora ou bijetora. Justifique suas respostas.
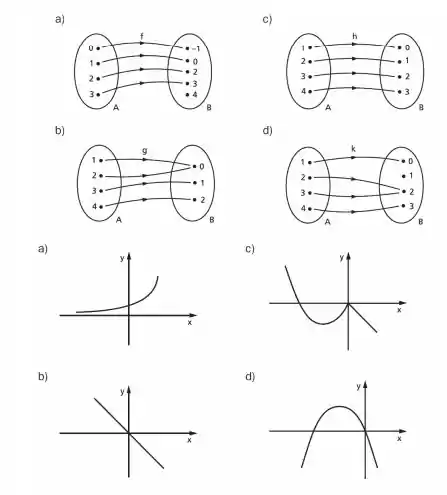
Questão 27
Seja a função definida por .
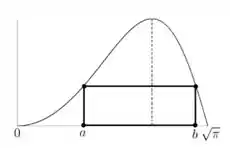
 A este item um aluno deu a seguinte resposta:
A este item um aluno deu a seguinte resposta:
Corrija a resolução do aluno e determine corretamente a área do retângulo em termos de .
Ver solução completaQuestão 28
Se é uma função diferenciável tal que e em .
d) A função possui inversa? Justifique.
Ver solução completaQuestão 29
Dados os conjuntos e , diga qual das relações abaixo definem uma função . Para cada uma destas diga se é injetora, sobrejetora ou bijetora.
Questão 30
7. Assinale a alternativa verdadeira.
- Se é sobrejetora, então é sobrejetora.
- Se e são funções sobrejetoras, então é sobrejetora.
- Se e são funções injetoras, então é injetora.
- Se e são funções injetoras, então é injetora.
- Se é sobrejetora, então possui inversa.
Questão 31
4. Seja a função definida por
Podemos afirmar que:
- é sobrejetora mas não é injetora;
- é injetora mas não é sobrejetora;
- é bijetora;
- ;
- Nenhuma das afirmações anteriores é verdadeira
Questão 32
Considere a função cujo gráfico é dado a seguir e faça o que se pede
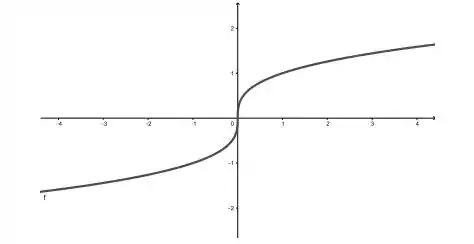
Justifique a afirmação é uma função injetora;
Ver solução completaQuestão 33
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 34
Considere a função cujo gráfico é dado a seguir e faça o que se pede
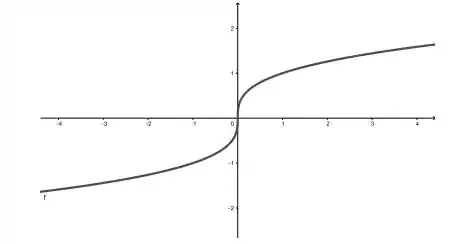
Estime o valor de .
Ver solução completaQuestão 35
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
Se e dada por:
Ver solução completaQuestão 36
Mostre que as funções definidas são bijetoras e determine a sua função inversa.
tal que .
Ver solução completaQuestão 37
Sejam dados e conjuntos não vazios.
- Defina rigorosamente o conceito de função de em
- Defina rigorosamente os conceitos de função injetora, sobrejetora e bijetora.
Questão 40
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 41
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 43
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
Se e dada por:
Ver solução completaQuestão 49
Sejam dada por e sua função inversa. Calcule em termos de . Calcule .
Ver solução completaQuestão 51
Dentre as alternativas abaixo, aquela que contém um polinômio que define uma função
bijetora de R em R é:
Ver solução completaQuestão 53
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 54
Para cada uma das seguintes funções, determine se são injetoras, sobrejetoras ou bijetoras, justificando.
,
Ver solução completaQuestão 55
Mostre que as funções definidas são bijetoras e determine a sua função inversa.
tal que .
Ver solução completaQuestão 56
Mostre que as funções definidas são bijetoras e determine a sua função inversa.
tal que .
Ver solução completaQuestão 57
16. Considere as afirmações:
- é uma função ímpar.
- é injetora.
- para todo
São verdadeiras:
- Todas
- Apenas I e II
- Nenhuma
- Apenas I e III
- Apenas II e III