Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 40
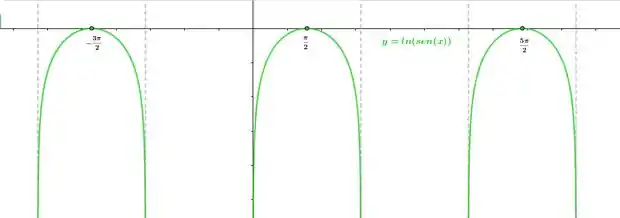
Faça o gráfico da curva
Passo 1
Inicialmente vamos considerar e observar o que essa função tem a nos “dizer”.
Observe que o domínio de corresponde somente ao conjunto dos números Reais positivos , isso porque a função não está definida para números negativos.
Sendo assim, o gráfico de está limitado à .
Passo 2
Em seguida verificaremos, se possui raízes, ou seja, se o gráfico toca o eixo
Para isso, é importante lembrar que Dessa maneira para encontramos as raízes fazermos com que o , que este se trata do argumento da função
Com isso ,percebemos que teremos várias raízes para ,pois como é uma função periódica há inúmeros valores que fazem com que o seno atinja seu máximo , ou seja ,. Alguns exemplos são:
Entre vários outros .Desse modo, o gráfico de toca o eixo várias vezes.
Passo 3
Determinaremos agora e , para em seguida verificarmos se possui máximos, mínimos ou pontos de inflexão. Dessa maneira temos que,
Pela regra da cadeia teremos,
Calculando a segunda derivada utilizando a regra do quociente,
Usando a identidade trigonométrica fundamental temos,
Passo 3
Vamos agora identificar se possui pontos críticos
Em relação aos pontos de críticos temos que
Sabemos que o se anula em onde é um inteiro ímpar.
Sendo assim temos vários candidatos à pontos críticos, vamos verificar se há mudança de sinal nas proximidades deles.
Perceba que, para valores dentro do intervalo , assume valores positivos (cresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, é um ponto de máximo no intervalo de
Passo 4
Vamos agora identificar se possui pontos de inflexão
Em relação aos pontos de inflexão temos que
Porém não há valor que satisfaça a igualdade acima, sendo assim, não possui pontos de inflexão. Consequentemente não possui mudança de concavidade.
Passo 5
Para finalizar verificaremos se possui assíntotas verticais ou horizontais.
No que se refere as assíntotas horizontais temos que
Logo, não possui assíntotas horizontais.
Um fato importante a ser lembrado é a respeito da função, é que o não é definido, ou seja, é uma indeterminação matemática.
Sendo assim, em relação as assíntotas verticais, perceba que como o argumento de é a função , que é uma função que se anula em valores que sejam múltiplos de isto é, onde é inteiro Dessa maneira, se calculássemos o limite em cada um desses pontos veremos que :
Logo, possui assíntotas verticais em onde é um número inteiro.
Resposta
