Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 80
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.
80.
Passo 1
Inicialmente, o que precisamos fazer é plotar esses gráficos para determinarmos as regiões compreendidas entre eles, ok? Se plotarmos os gráficos, teremos:
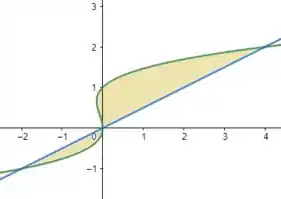
No qual a função em verde é e a função em azul é . Uma vez plotados, o que precisamos descobrir é a área dessas rachuras aí, certo? Assim como discutido na seção 6 do George, os intervalos de integração para uma são , que são intervalos verticais (em ), não mais horizontais (em ). Além disso, temos que descobrir os pontos em que as funções se encontram para descobrirmos nosso intervalo de integração, beleza? Sabendo dessas informações, nosso problema fica bem mais tranquilo! Então bora lá!
Passo 2
Temos que descobrir os pontos em que as funções se encontram para sabermos quais serão os limites de integração da nossa integral, galera! Para descobrirmos, basta igualarmos as duas funções, olha só:
Para que esse produto dê zero, tem que ser 0 ou tem que ser 0, não é mesmo? Então precisamos resolver essa equação do segundo grau também, bora lá!
Sendo assim, podemos escrever nossa equação da seguinte maneira:
Dessa forma, assim como podemos notar na figura do passo 1, teremos que descobrir o valor de 2 integrais, cujos intervalos de integração acabamos de encontrar!
Passo 3
Para calcularmos a área de uma região em relação à , assim como discutido na seção 6 do George, o que precisamos descobrir é quais são as curvas à direita e à esquerda. Depois de descoberto isso, basta fazermos:
Onde, nesse caso, seria a curva à direita e seria a curva à esquerda.
Para a primeira região rachurada da figura do passo 1, a curva mais à direita é e a curva mais à esquerda é . Ademais, o intervalo é .
Para a segunda região rachurada da figura do apsso 1, a curva mais à direita é e a curva mais à esquerda é . Ademais, o intervalo é .
Passo 4
Agora que já temos TUUUDO que precisamos, basta escrevermos as integrais, se liga:
Lembrando que para resolvermos todas essas integrais, a única regra que utilizamos foi:
Passo 5
Sendo assim, a área total será a soma de todas essas áreas. Portanto, temos que: