- Faça o gráfico da função
- Qual o domínio e a imagem de ?
-
é uma função periódica? Justifique sua resposta.
Passo 1
E aí, pessoas! Bora pra mais uma?
Na letra (a) ele quer que você apenas monte o gráfico, sem mistérios.
Na letra (b) você vai dizer qual é o domínio (de onde ele parte) e a imagem (somente os valores em que ela chega) da função.
E na letra (c) você vai verificar se ela tem um certo padrão.
Bora lá?
Passo 2
(a)
A letra (a) é a mais direta. O gráfico da função é meio doidão. Fica assim:
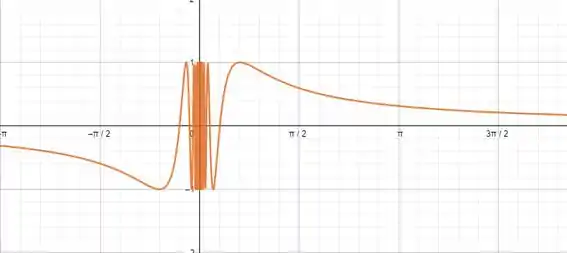
Passo 3
(b)
Pra achar o domínio, é só ver onde que ela tá definida no eixo . Parece que pode ser qualquer , né? É aí que você se engana! Se eu jogar deixa de ser função, porque eu estaria dividindo 1 por 0 e não pode isso. Então o domínio são todos os reais, menos o 0.
E a imagem é onde tá chegando. Tá vendo que só tá indo de -1 a 1? Então:
Passo 4
(c)
Dá pra ver de cara que ela não é periódica, porque ela não apresenta um padrão único pra qualquer pedaço. Mas vamos supor que ela seja periódica e o período seja T, ok?
A função dada foi . Vamos jogar ali dentro, onde é o período e é a quantidade de vezes que esse período vai ser somado. Por que isso? Porque eu sei que o valor da função pra um ponto e o valor dela pra tem que ser iguais, porque vão corresponder a pontos iguais (já que, no gráfico, são pontos que levam no mesmo y). Como vale pra qualquer x, vale pra um x arbitrário, como .
Agora, vamos pegar um tão grande que faça com que >, por exemplo.
Passando o como multiplicação e o como divisão: . Só que nunca pode ser zero, porque o denominador não é zero, e a gente tá pegando um muito grande positivo. Então:
Logo:
, o que é uma contradição, porque a gente viu que tinha que ser igual a zero.
Pronto :)
Resposta
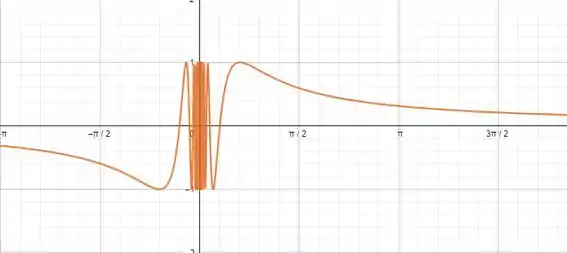
(b) ,
(c) Ela não é periódica