Funções Trigonométricas – Parte 1
Teoria
Você se lembra daquelas relações trigonométricas? Então, vou relembrar contigo as principais,
O (teta) era um ângulo maroto de um triângulo retângulo, nós identificávamos a hipotenusa e os catetos e usando as fórmulas, nós fazíamos as continhas.
Mas o que acontece se transformarmos cada uma das relações que tínhamos anteriormente em funções? Ou seja, o que acontece à medida que variarmos o valor de x, para as seguintes funções?
Precisamos então entender como cada uma das funções vai se comportar e nesse sentido, precisamos falar sobre algo em especial: Periodicidade.
Periodicidade das funções trigonométricas
Antes de tudo: O que é uma função periódica?
Uma função periódica é uma função que se repete dentro de um intervalo no eixo .
Ainda não entendeu? Vamos ver um exemplo!
Observe o gráfico abaixo e veja como a função se repete:
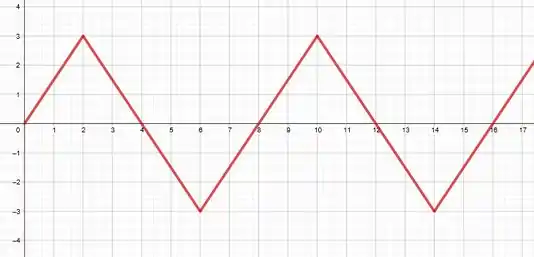
Olhando pra esse gráfico, percebemos por exemplo que para , temos , e quando também temos . Agora, você consegue me dizer qual o próximo valor de nos retornará ?
Se você respondeu , parabéns! :D
Se não respondeu, fica tranquilo. Você vai entender agora...
Na verdade, a gente consegue fazer essa previsão porque encontramos um mesmo valor de repetido de 8 em 8 unidades de .
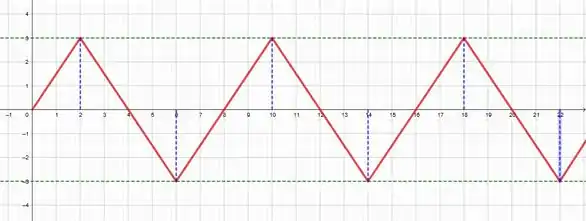
Então, assim como
e
Podemos prever que
Shooooow?
Então chamaremos esse 8 de PERÍODO!
Podemos ver isso no gráfico, o mesmo formato vai se repetindo de 8 em 8 unidades de x, ou seja, para construirmos o gráfico de uma função periódica basta construirmos o gráfico para um período da função, pois o resto do gráfico será a repetição dessa parte.
Formalizando um pouco mais, temos que uma função é chamada de periódica quando:
Para todo .
E o menor valor de que satisfaz a condição acima é chamado de período da função .
Já vimos que as relações trigonométricas são exploradas para um círculo, que chamamos de círculo trigonométrico. Isso explica por que essas funções são periódicas, já que à medida que vamos dando voltas no círculo, vamos voltando a encontrar os mesmos valores para o y.
Agora estamos preparados para falar de cada uma das funções trigonométricas.
Função Seno
A função seno será dada por
Como falamos anteriormente, os valores possíveis para o estarão dentro do ciclo trigonométrico, que está representado abaixo:
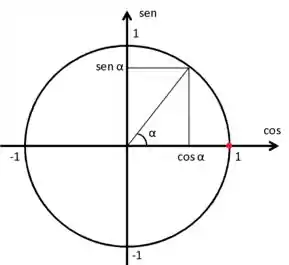
Vamos relembrar alguns detalhes importantes do círculo trigonométrico: o eixo é o eixo dos senos e o eixo x é o eixo dos cossenos. Além disso, em radianos, uma volta completa no círculo vale e as medidas dos ângulos começam a partir do ponto vermelho e indo pra cima, no sentido anti-horário.
Com isso, podemos dizer que o seno terá valores extremos para ângulos de (ponto mais alto do círculo) e (ponto mais baixo do círculo), onde a função vale:
A função ficará oscilando entre esses valores, sendo que não há nenhuma indeterminação no intervalo e isso se repete indefinidamente.
Dessa forma, já podemos afirmar que o domínio da função seno (valores possíveis para o ) é o conjunto dos números reais, ou:
Já para a imagem (valores resultantes em , vimos que a função vai estar sempre entre -1 e 1. Isso significa que
Lembrando que teremos isso quando .
Mas e se tivermos
Perceba que, nesse caso, todos os valores de que tínhamos anteriormente vão ser multiplicados por 2, isso significa que agora nossa função terá valores máximo e mínimos em , respectivamente.
Isso vai acontecer sempre que tivermos a função seno multiplicada por uma constante, então podemos generalizar:
Para .
Ah, mas por que precisa ser diferente de zero?
Simplesmente porque zero multiplicado por qualquer coisa será igual a zero e nesse caso, a função valeria zero para qualquer valor de .
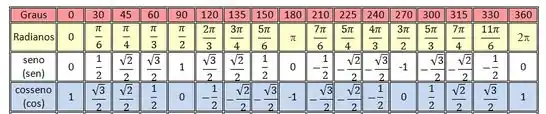
Para esboçar o gráfico da função seno, vamos usar alguns valores conhecidos da função usando os chamados “ângulos notáveis” e algumas relações do círculo trigonométrico. Juntei tudo nessa tabelinha abaixo:
Agora, marcando esses pontos no gráfico e ligando para formar nossa curva, teremos essa belezinha aqui
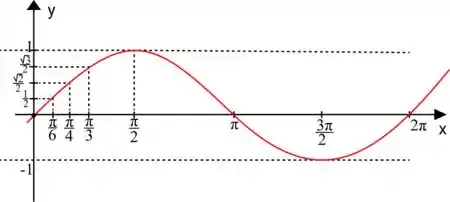
E um fato extremamente interessante é que essa curva continua se repetindo indefinidamente, à medida que aumentamos ou diminuímos os valores de x:
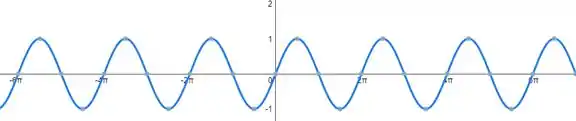
Obs: Esse de qualquer função trigonométrica SEMPRE será dado em radianos, assim como fazemos no círculo trigonométrico. Não se esqueça disso!!!
Observe que o gráfico se repete de em o que isso significa?
O PERÍODO DA FUNÇÃO SENO É !!!
Mas qual será o período de uma função como essa daqui:
Para achar o período da função, pegamos o argumento, que é tudo que fica dentro do seno, substituímos o pelo que é a letra que representa o período e igualamos isso a , que é o período da função . Olha só:
Vamos comparar os gráficos!
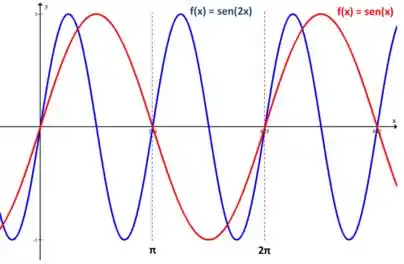
Repara que a curva azul, que representa , se repete duas vezes no intervalo que a vermelha, que representa repete uma só. Isso acontece porque o período de é a metade do período de !
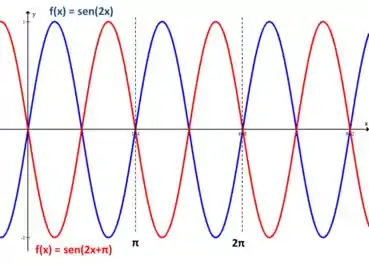
Mas e se tivéssemos
Repetindo aquele procedimento, temos
E quando temos números somando ou subtraindo dentro do seno, podemos ignorar esse valor! Igualamos a só a parte que multiplica . Então,
O termo que soma apenas desloca a função um pouquinho pro lado, mas o período é o mesmo. Vamos dar uma olhada no gráfico!
Função Cosseno
A função cosseno é dada por:
Ela funciona de um jeito MUITO parecido com a função seno, então muito do que vimos até aqui podemos estender pra função cosseno, por exemplo: o domínio da função cosseno também é dado pelo conjunto dos números reais:
E, assim como o seno, os valores que saem da função também oscilam entre , por isso a imagem também é:
E quando tivermos uma constante multiplicando a função, ficamos com:
O gráfico dessa belezinha será igual ao do seno, mas um pouco deslocado e nós montamos ele da mesma forma que fizemos no da função seno, mas agora usando os valores que temos para o cosseno. Observe que temos os mesmos números aparecendo nas duas funções, só que em lugares diferentes:
Marcando esses pontos num gráfico, temos
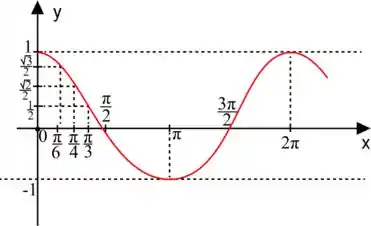
E se expandirmos a construção desse gráfico para a esquerda e direita, temos
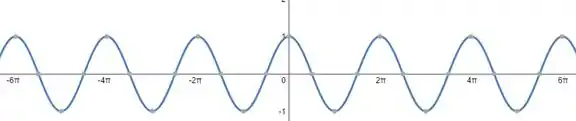
A função cosseno também é periódica, se repetindo a cada , que é a medida de uma volta completa no círculo trigonométrico, assim como o seno! E da mesma forma, se o argumento da função cosseno mudar, a gente pode calcular o período fazendo o mesmo procedimento:
Função Seno
Função Cosseno
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Diga se as afirmações abaixo são verdadeiras ou falsas:
- O seno de um ângulo é calculado através da fórmula ;
- O cosseno de um ângulo é calculado através da fórmula ;
- As relações são definidas a partir de um triângulo retângulo.
- A tangente de um ângulo é calculada através da fórmula
Passo 1
Fala Aíí!! Vamos analisar cada uma das afirmações e verificar quais são verdadeiras e quais são falsas!
Na letra (a) temos a afirmação “O seno de um ângulo é calculado através da fórmula .
Vamos relembrar o que é o seno de um ângulo?
O é a razão entre a medida do cateto oposto e a hipotenusa de um triângulo retângulo. Ou seja, é o resultado da divisão da medida do cateto oposto pela medida da hipostenusa
Pra lembrar a gente pode até brincar com as palavras. Olha para o ângulo e para o cateto oposto, você concorda que o cateto oposto está longe do ângulo? Então, podemos lembrar que ele está “sem” o ângulo, assim a relação dele com a hipotenusa é o “seno”.
Ou seja, o nosso é
Assim, a afirmação da letra (a) é falsa!
Passo 2
b) Para verificar se a afirmação da letra (b) é verdadeira ou falsa vamos relembrar o que é o cosseno de um ângulo . O cosseno é a razão entre a medida do cateto adjacente a e a hipotenusa do triângulo. Visualmente, teremos
E aqui também tem aquele joguinho de palavras. Olha para o ângulo e para o cateto adjacente, você concorda que o cateto adjacente está “colado” no ângulo? Então a relação entre a hipotenusa e o cateto que está “colado” no ângulo é o “cosseno”.
Assim,
Ou seja, a afirmação é verdadeira!
Passo 3
c) A afirmação que devemos avaliar se é verdadeira ou falsa é “As relações são definidas a partir de um triângulo retângulo.” Essa afirmação é verdade, pois o relacionam as medidas dos lados de um triângulo retângulo com as medidas de seus ângulos.
Lembrando que um triângulo é retângulo quando um de seus ângulos é igual a .
Passo 4
d) A última afirmação se refere a tangente de um ângulo . A tangente é a única relação que não envolve a hipotenusa de um triângulo. Ela é dada por
Onde, no triângulo retângulo
Ou seja, a afirmação da letra (d) é falsa!!
Resposta
- Falsa
- Verdadeira
- Verdadeira
- Falsa
Exercício Resolvido #2
Elaboração Própria
Determine o domínio e a imagem da função e esboce seu gráfico.
Passo 1
Vamos lááá! Primeiro vamos determinar o domínio da função
Sabemos que o domínio da função é o conjunto dos números reais, certo?!
Assim, se você reparar, na função do nosso enunciado, estamos apenas somando , o que não interfere no domínio. Assim, ele continuará sendo o conjunto dos números reais. Portanto,
Beleza?!
Passo 2
Agora vamos determinar a Imagem da função .
Como podemos fazer isso??
Vamos substituir os valores máximo e mínimo de e assim a imagm será o intervalo entra esses dois valores, beleza?!
Bom, a função varia entre e
Assim,
Aplicando esses valores na função , temos
Para :
Da mesma forma, para :
Portanto, a Imagem de é:
Show de bola?!
Passo 3
Para esboçarmos o gráfico da função, basta esboçarmos o gráfico de e somarmos 2 a cada ponto. Ou seja,vamos transladar o gráfico para cima 2 casas:
Show de bola?!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração Própria
Determine as imagens das funções abaixo:
Passo 1
Opaaaaa! Precisamos determinar a imagem de cada uma das funções, certo?!
Então vamos lá!
Na letra (a) temos a função.
A função está entre e :
Agora vamos multiplicar essa desigualdade toda por , pois o que queremos saber é a variação da função , lembra?
Assim,
Ou seja, a .
Passo 2
b) Na letra (b) temos a função .
Sabemos que a função deve estar entre e :
Certo? Como a nossa função é então vamos dividir toda a desigualdade por
Olha aíí!! Dessa forma, . Show de bola?!
Passo 3
- Vamos seguir o mesmo raciocínio para !!
Sabemos que a função está entre e :
Agora vamos multiplicar a desigualdade por :
Assim,
Ou seja,
Passo 4
Pra fechar com chave de ouro, para a função da letra (d) vamos utilizar o mesmo raciocínio!!!
Se
Então, basta multiplicarmos toda a desigualdade por :
Assim,
Ou seja, .
Show de bola?!?!
Resposta
- .
Exercício Resolvido #4
Elaboração Própria
Determine o valor de
Passo 1
Vamos lá!! Temos uma tabelinha que podemos carregar para qualquer lugar com os valores dos principais ângulos e seus valores:
Beleza?! Guarda no coração essa tabelinha!! Nessa questão iremos utilizá-la!
Passo 2
Não sabemos o valor de , mas podemos reescrever da seguinte maneira
Concorda?!
MAS PERAAAAA!!!!!
NÃO podemos apenas subtituir os valores e somar!! Como estamos querendo calcular o seno da soma temos uma regrinha a seguir!! É essa aqui ó
Lembra sempre disso! Não podemos apenas substituir e somar os valores dentro do seno, precisamos usar a fórmulinha acima!!
Passo 3
Assim,
Agora podemos usar os valores da tabelinha que devem estar no nosso sangue!!!
Substituindo os valores, teremos
Beleza?!
Podemos fazer a multiplicação
Show de bola?!?!
Resposta
Exercício Resolvido #5
Elaboração Própria
Determine o valor de
Passo 1
OPAAA!! Queremos calcular o , certo?! Lembra que a função é uma função periódica? Ela vai se repetir depois do ou , lembra?
Então vamos quebrar o em duas parcelas para facilitar a nossa vida!! Vem comigo!
Passo 2
Vamos fazer o seguinte. Como a função é periódica
Sabemos que , basta olhar para o círculo trigonométrico:
Beleza?!
Assim,
Passo 3
Para encontrar o valor de basta olharmos pra tabelinha com o valor dos principais ângulos
Portanto,
Show de bola?!?!
Resposta
Exercício Resolvido #6
Elaboração Própria
Determine o período das seguintes funções:
Passo 1
O período () de uma função é o intervalo que ela demora em se repetir. Olhando para o gráfico da função cosseno, podemos ver que ela se repete no intervalo de até .
Então, o período da função cosseno é sempre .
Passo 2
-
O período do cosseno é sempre , então toda vez que variar em , teremos a função se repetindo. Isso é a mesma coisa que dizer que é igual a .
Então, agora igualamos seu argumento a esse valor:
Só isso mesmo!
Passo 2
Novamente, vamos chamar de e igualar seu argumento a esse valor:
Passo 3
c)
Aqui a gente segue os mesmos passos: o período do cosseno é sempre , então chamamos de e igualamos seu argumento a esse valor.
Mas, agora, CUIDADO! Neste caso, o indica somente que a função está deslocada unidades para a direita.
Portanto, o período não é afetado e será:
Passo 4
d)
Na soma de seno e cosseno, o período continua sendo e, portanto:
Resposta
Exercício Resolvido #7
Elaboração própria
Simplifique a função abaixo:
Passo 1
Relembrando, sabemos que a Equação Fundamentalda Trigonometria nos diz:
Isolando o , teremos:
Opa! Acabamos de ver uma relação para expressão do nosso denominador.
Passo 2
Passando a raiz dos dois lados, teremos:
Agora sim, substituindo lá, teremos:
Porém a função só está definida para valores de [para pois nesses valores e teríamos uma indeterminação.
Resposta
Exercício Resolvido #8
UFRGS 2018
Um ponto A que se movimenta sobre uma circunferência, tem sua posição considerada na vertical, no instante descrita pela relação para . Nesse caso, a medida do diâmetro dessa circunferência é:
a) 30
b) 40
c) 50
d) 80
e) 120
Passo 1
Bom, ele deu a equação da posição vertical. Vamos ver o que conseguimos fazer com isso?
Lembra que a função seno pode assumir como valor máximo e como valor mínimo? Para quem não lembra, olha o gráfico dela ai embaixo,
Vamos usar esse mesmo raciocínio para achar o nosso e . Lembra que nós temos essa função,
O valor máximo da posição vertical vai ser quando o seno for mínimo. Ou seja:
Do mesmo jeito, a posição vertical vai ser mínima quando o seno for máximo:
Passo 2
Beleza, mas o que podemos fazer com essa informação?
Esse ponto A que ele tá falando no enunciado tá se movimentando de acordo com uma função trigonométrica, assumindo valores sempre maiores que 80 e menores que 120. Mas sempre dentro desse intervalo.
E como a função é PERIÓDICA, ele fica repetindo esse movimento de vai-e-vem, descrevendo uma circunferência (como disse o enunciado).
Aí que vem o pulo do gato!
Vamos traçar uma linha horizontal onde temos o e e colocar uma circunferência entre essas linhas, pois a nossa função varia sempre dentre desse intervalo,
Repara que ao fazermos isso, a gente consegue identificar qual seria o diâmetro da circunferência. E o diâmetro vai ser dado pela diferença do ponto máximo para o ponto mínimo, ou seja:
Ou seja, . LETRA B
Resposta
Letra B
Exercício Resolvido #9
Ueg 2019 (Adaptada)
Quais são os valores de , sendo , para os quais as funções e se interceptam?
Passo 1
Vamos lá, as nossas duas funções vão se interceptar quando
Ou seja
Vamos melhorar isso passando o para o outro lado dividindo, assim ó
Passo 2
Agora basta lembrarmos que . Então, teremos:
Basta pegarmos então os valores para os quais a será igual a 1. Teremos esses valores para.
Escrevendo isso em radianos, pra ficar padrão... teremos:
Resposta
Exercício Resolvido #10
Elaboração Própria
A figura mostra o gráfico da função f, dada pela lei
Qual o valor de a e b indicados no eixo x?
Passo 1
Acho que você concorda comigo que essa função não está nada amigável e receptiva, está bem complicado de chegarmos a alguma conclusão sobre ela.
Vamos tentar simplificar?
Fazendo esses produtos notáveis, temos
Beeeem mais bonitinha, né? =D
Passo 2
Beleza, agora precisamos ver os pontos do primeiro quadrante que terão o , como nos mostra o enunciado. Basta igualarmos a nossa função a . Fica assim ó:
Dividindo os dois lados por 2, temos:
Tá, mas no que isso adianta a gente?
A expressão que está ao lado esquerdo é igual ao seno de um arco duplo, portanto, teremos:
Agora, pensa comigo no seguinte, quais são os valores que tem como o seno o ?
O seno de 60° e o de 120° graus, por estarem no 1º e 2º quadrantes, são positivos.
Ou seja, teremos:
Concluimos então que
Resposta
e