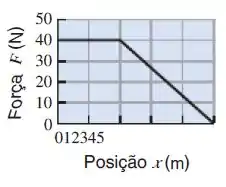
Uma força variável , no sentido positivo do eixo , tem seu gráfico mostrado abaixo. Encontre o trabalho realizado pela força sobre uma partícula que se move de a .
Passo 1
Precisamos achar o trabalho realizado por uma força. A gente sabe que o trabalho, quando temos uma força variável, é dado por:
Então o que precisamos fazer é calcular essa integral de até :
Passo 2
Mas repara que calcular a integral de uma função é o mesmo que calcular a área entre a curva que ela descreve e o eixo . Então podemos escrever:
Podemos aproximar essa área por um triângulo (de base e altura mais um retângulo (de base e altura 40):
Conseguimos!