Integral Do Trabalho De Uma Força
Teoria
Fala aí! Nesse texto sobre aplicações de integrais, vamos ver como usar essa ferramenta do Cálculo para calcular fenômenos físicos, mais especificamente a integral do trabalho de uma força.
Tá preparado? Então vem comigo ver como fazer isso aí com uns exercícios resolvidos passo a passo 😋
⭐ Veja também ⭐
Como calcular o trabalho usando integral?
A fórmula mais simples de trabalho é aquela da força vezes deslocamento.
Mas essa fórmula aí só pode ser usada quando a força
É aí que entra a integral!
Olha só, imagina uma força variável qualquer, com uma função que descreve esse gráfico aqui em relação à distância:
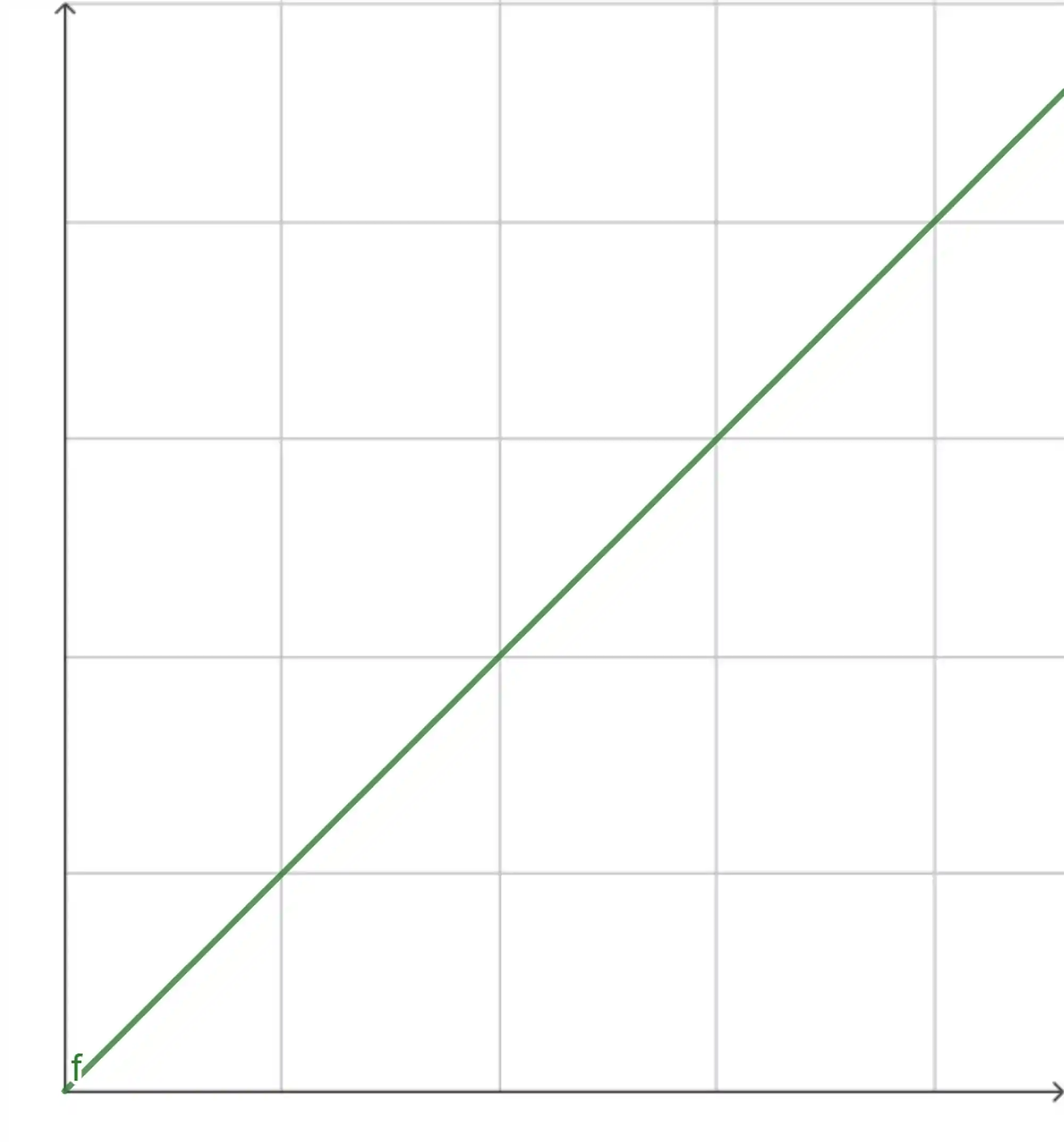
Consegue perceber que cada valor de distância ali no eixo
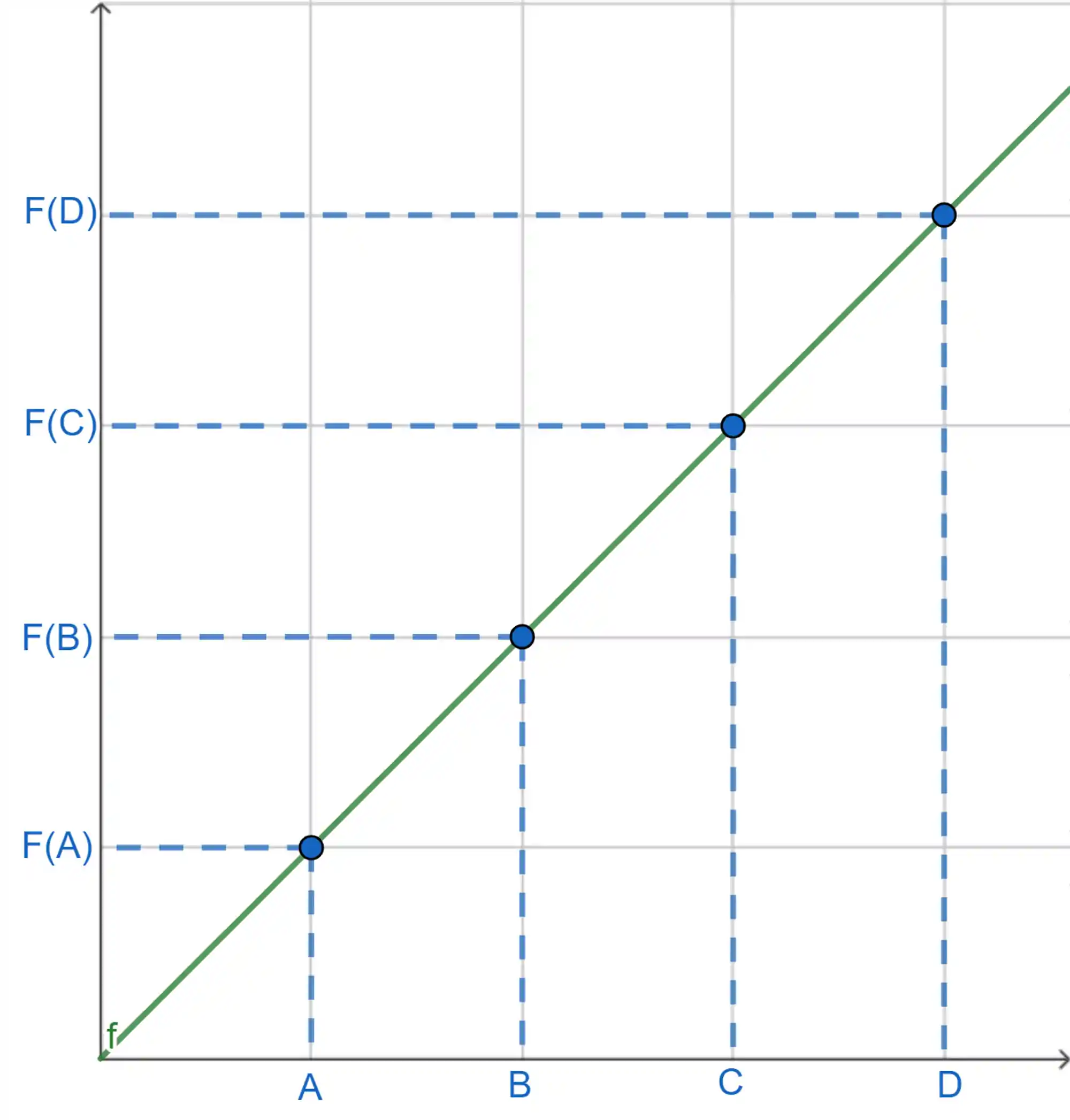
Isso que quer dizer a força ser variável!
Agora, olha só como a gente resolve isso. Se a gente pegar um pedacinho muito pequeno (infinitesimal) de deslocamento
E aí podemos calcular o trabalho também infinitesimal
Beleza, mas a gente quer o trabalho todo e não só esse pedacinho, não é? Então, pra voltarmos de
Ah, é claro, a gente tem que conhecer a expressão da força
Então, bora ver alguns exemplos com os casos mais comuns.
Exemplo 1 - Trabalho da Força Peso
Qual o trabalho realizado para içar um balde que pesa
Tá, se queremos o trabalho de uma força em dada direção, temos que encontrar uma expressão para essa força nessa direção. O primeiro passo é descobrir qual força atua nesse caso.
Repare que, pelo enunciado, a massa da corda não é desprezível. Isso significa que o trabalho realizado aqui vai ser o necessário para levantar o sistema
- Peso do balde
- Peso da corda
- Força para içar
Se o sistema é içado com velocidade constante, quer dizer que o somatório das forças sobre ele é nulo (Segunda Lei de Newton), certo? Então, a força para içar
O peso do balde já foi dado pelo enunciado. Vale
Aí tem que tomar cuidado! Conforme a corda vai sendo puxada, uma parte cada vez menor dela faz peso.
Se estabelecermos o seguinte sistema de coordenadas:
Conforme a corda vai sendo puxada, o comprimento que resta é
Lembrando que esse sistema de coordenadas aí é você quem escolhe, só tem que se atentar pra ser sempre coerente com ele.
Então, o peso da corda vai ser dado por:
Agora sim, bora substituir lá outra expressão.
A força atua por
Integrar esse polinômio aí não tem segredo, né?
Agora aplica os limites de integração:
Exemplo 2 - Trabalho da Força Elástica
Determine o trabalho necessário para esticar uma mola partindo de seu comprimento inicial de
Novamente, o primeiro passo é encontrar a função que descreve a variação da força em
Como a situação aqui envolve uma mola, estamos tratando da força elástica! E, como você deve saber, esse cara pode ser descrito pela Lei de Hooke:
Então é essa expressão aí que vamos usar.
E os limites de integração?
Bora definir o seguinte sistema de coordenadas:
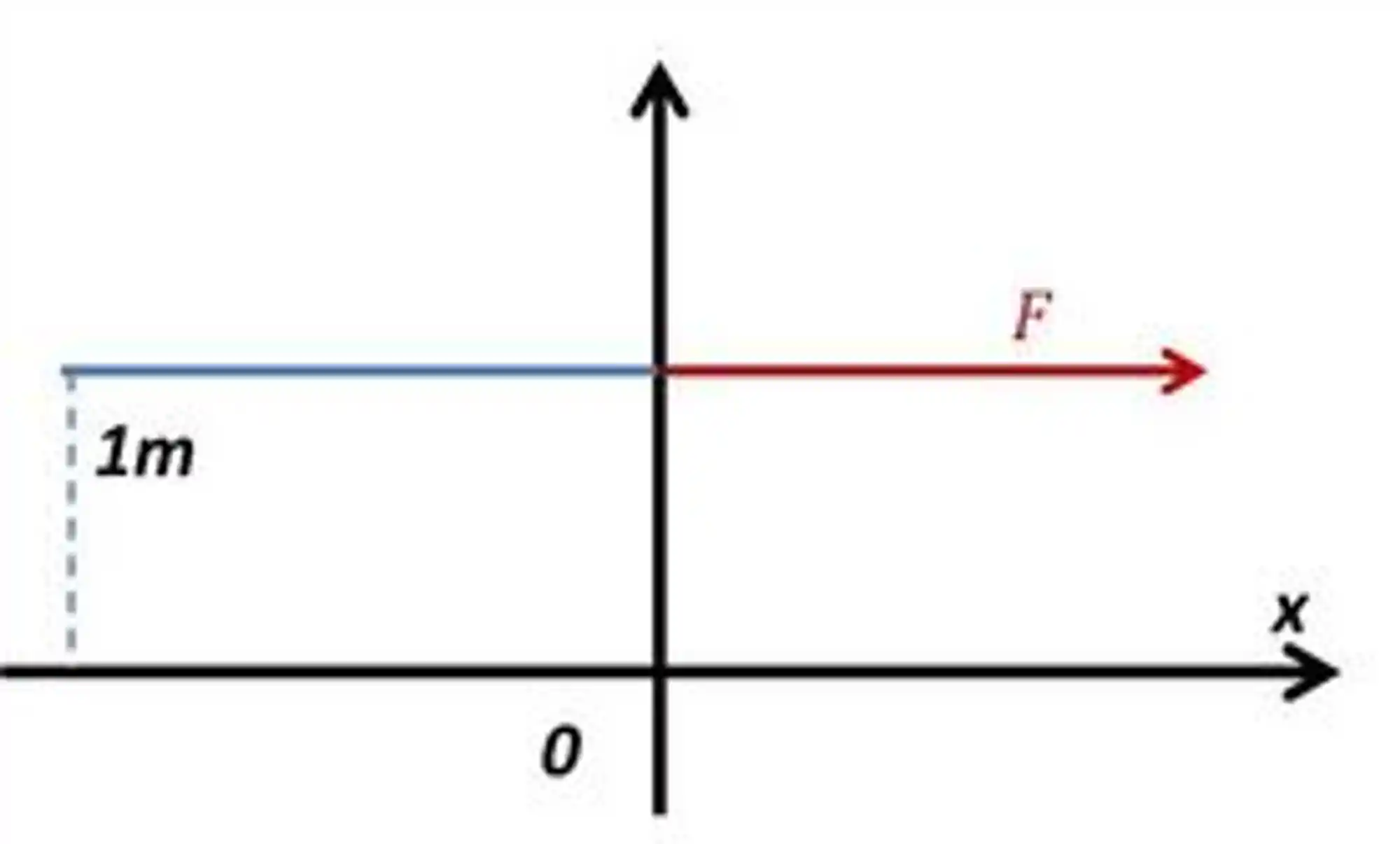
Como o enunciado quer que a mola seja esticada
Com mais algumas continhas:
Pronto! Chegamos no nosso resultado.
Deu pra perceber que o sucesso na resolução de problemas que pedem o trabalho realizado por uma força variável depende de entender a situação para podermos extrair uma função e escolher o sistema de coordenadas de forma que facilite suas contas, né?
Então bora fazer mais alguns exercícios resolvidos passo a passo pra ficarmos bem craques nisso aí!
Exemplo 1 - Trabalho da Força Peso
Exemplo 2 - Trabalho da Força Elástica
Exercícios Resolvidos
Exercício Resolvido #1
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, 485 - 7
Use a integral abaixo
para determinar o trabalho realizado ao comprimir o gás de a , se e e obedecem à lei dos gases (para processos adiabáticos).
Passo 1
Primeiro, uma observação: as unidades são estranhas, eu sei. Esquece elas, usa os números e no final te conto qual será a unidade final.
Dada a fórmula, a boa é se conseguirmos escrever a pressão apenas em função do volume. Dado a equação do processo adiabático que o cara nos deu, podemos escrever:
Onde é a constante que tem na equação que o enunciado nos deu. Com isso, tendo o volume inicial e final, sabemos a fórmula do trabalho:
Passo 2
Integrando, teremos:
Antes de fazer essa conta gigante, vamos descobrir . Pelo enunciado, temos pressão inicial e volume inicial. Com isso, é fácil descobrir o valor de pela fórmula que o cara nos deu:
Então:
É claro que vou usar uma calculadora para calcular esse monstrengo estranho. Cheguei no seguinte aqui:
A unidade final é essa aí, libra-polegada
Resposta
Exercício Resolvido #2
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, 489 - 38
Dois elétrons longe um do outro metros repelem-se com uma força de
Suponha que um elétron seja mantido fixo no ponto no eixo (unidades em metros). Quanto trabalho será necessário para deslocar um segundo elétron ao longo do eixo do ponto para a origem.
Suponha que um elétron seja mantido fixo em cada um dos pontos e . Quanto trabalho será necessário para deslocar um terceiro elétron ao longo do eixo de a ?
Passo 1
A gente sabe que o trabalho será dado pela integral na distância do produto . Nesse problema, nossa variável de integração será . Pela equação do trabalho, teremos:
Onde o posição inicial será e a final será . Assim, a distância ao outro elétron em inicialmente e no fim serão dadas por:
Então, os limites de integração serão dados por:
Passo 2
Substituindo a força, teremos:
O trabalho tem sinal negativo pois é realizado sobre o sistema, ou seja, vai contra a tendência natural do movimento, de se repelir. O usual mesmo é usar seu módulo:
Passo 3
Temos o mesmo princípio a ser aplicado nessa letra, apenas muda que calcularemos duas integrais ao invés de uma.
Em relação ao elétron em , os valores de inicial e final serão:
Para o em , serão:
O que teremos, então, será:
Por propriedades das integrais, teremos:
Passo 4
Substituindo a força, teremos:
O trabalho tem sinal negativo pois é realizado sobre o sistema, ou seja, vai contra a tendência natural do movimento, de se repelir. O usual mesmo é usar seu módulo:
Resposta
Exercício Resolvido #3
George B. Thomas, Cálculo Volume II, 11ª ed. São Paulo: Pearson Education do Brasil Ltda., 2009, 486 - 12
Suponha que o gás contido em um cilindro com área transversal esteja sendo comprimido por um pistão. Se for a pressão do gás em e o volume em , o trabalho realizado na compressão do gás, do estado até o estado é dado pela equação:
Use essa integral para determinar o trabalho realizado ao comprimir o gás de a , se e e obedecem à lei dos gases , para processos adiabáticos.
(Dica: Nas coordenadas sugeridas pela figura, . A força contra o pistão é )
Passo 1
Bem, ele quer o trabalho realizado para comprimir um gás de dado volume e dada pressão até outro estado. A integral a ser usada, ele já definiu no enunciado e é essa aqui embaixo:
Além disso, ele definiu a relação entre e nesse processo.
Nesse tipo de questão, o mais difícil é que, se não é constante, ou seja, se varia com o volume, temos que escrever em função de para poder integrar, já que a integral está definida para .
Nesse caso, ele deu a relação entre e . Então é essa relação que temos que usar para relacionar os dois e escrever em função de .
Passo 2
A primeira coisa que eu vou fazer é justamente escrever em função de .
Ele diz que:
Então:
Beleza, tá tudo muito bom, mas como achar essa constante ?
Repara que no estado inicial do gás, ele dá as duas condições do gás e . Logo, temos como substituir na fórmula e encontrar , não é mesmo?
Olha aqui:
Substituindo na fórmula:
Passo 3
Agora eu tenho que substituir na integral. Temos que lembrar que como a nossa variável de integração é , os limites de integração devem ser dados em função de .
Temos, do enunciado:
Logo:
- ''Passo 4
Resolvendo a integral:
O trabalho realizado pelo sistema é negativo porque se trata de uma compressão.
- ''