No início desta seção consideramos a função
e conjecturamos que quando com base em evidências numéricas. Utilize coordenadas polares para comprovar o valor do limite. Em seguida, faça o gráfico da função.
Passo 1
Eaeee, belezinha?? Bom... o enunciado nos deu a seguinte função:
O enunciado ainda nos disse como dado que quando .
Queremos utilizar coordenadas polares para comprovar o valor do limite. E, por fim, iremos esboçar o gráfico de .
Para isso, primeiramente precisamos lembrar a substituição que fazemos para trabalhar com coordenadas polares:
Agora bora aplicar!! 😉
Passo 2
Aplicando a conversão no nosso limite, temos:
Sabemos que , portanto:
Sabemos do limite fundamental que , portanto:
Passo 3
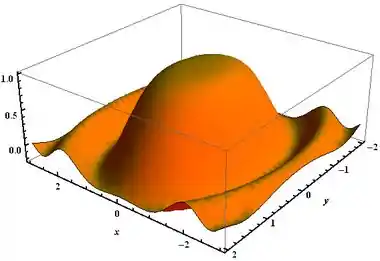
Show de bola, galera! Agora vamos só dar uma olhada no gráfico dessa nossas função para observar o seu comportamento.
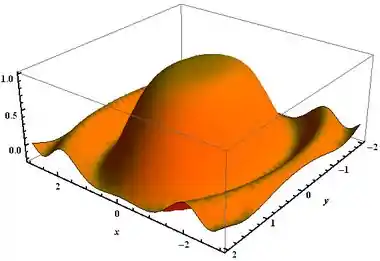
Perceba que no ponto o ponto de máximo da função é .
Resposta