Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 74
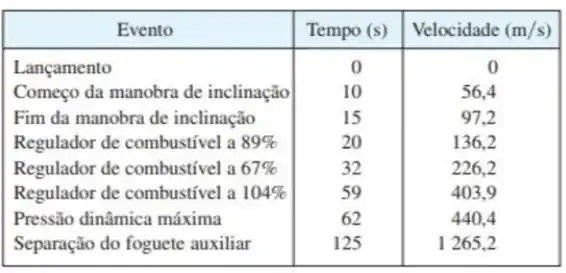
Em 7 de maio de 1992, o ônibus espacial Endeavour foi lançado na missão STS-49. A tabela a seguir fornece os dados da velocidade do ônibus entre o lançamento e a ejeção dos foguetes auxiliares.
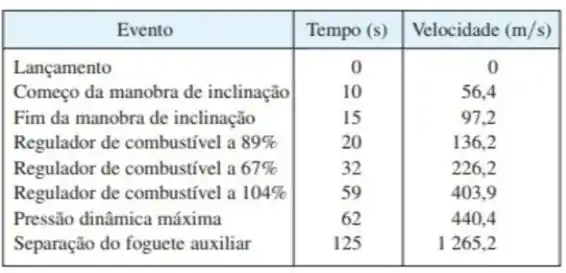
- Use uma calculadora gráfica ou computador para encontrar o polinômio cúbico que melhor modele a velocidade do ônibus para o intervalo de tempo . Faça então o gráfico desse polinômio.
- Encontre um modelo para a aceleração do ônibus e use-o para estimar os valores máximo e mínimo durante os primeiros 125 segundos.
Passo 1
Falaeee, belezinha?? Então... a questão nos dá uma tabela que relaciona o tempo com a velocidade de cada evento de um ônibus espacial.
A questão quer que usemos uma calculadora gráfica ou computador para encontrar o polinômio cúbico que melhor modele a velocidade do ônibus para o intervalo de tempo .
Em seguida devemos plotar o gráfico.
Também devemos encontrar um modelo para a aceleração do ônibus e usa-lo para estimar os valores máximo e mínimo durante os primeiros 125 segundos.
Passo 2
Utilizando uma calculadora gráfica, podemos modelar da seguinte maneira:
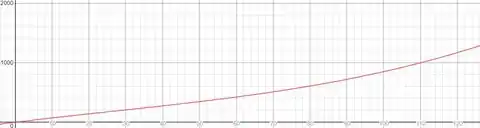
Passo 3
A aceleração basta derivarmos em relação ao tempo, daí ficamos com
Para encontrar os valores de máximo e mínimo da aceleração, basta derivarmos e igualarmos a zero, daí
Passo 4
Agora, de acordo com o método do intervalo fechado, temos que a aceleração máxima e mínima ou estará no ponto crítico, ou nos extremos do intervalo fechado.
Aplicando o método do intervalo fechado, precisamos calcular e
Logo, a aceleração máxima está em e vale e a aceleração mínima está em e vale .
Resposta
A aceleração máxima está em e vale e a aceleração mínima está em e vale