Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.4 - Ex. 70
Onde a função é derivável? Dê uma fórmula para e esboce os gráficos de e .
Passo 1
Queremos saber em que intervalo de a função é derivável.
Essa é uma função que o comportamento dela não é tão claro. Por isso, vamos substituir alguns valores nela e ver como ela se comporta.
São bons valores para a gente substituir aqueles que zeram os termos dentro dos módulos, provavelmente esses pontos serão importantes para a gente.
Além disso, vamos substituir valores dentro desse intervalo e fora dele para ver se obtemos algum tipo de comportamento interessante.Depois disso, montamos uma tabela e um gráfico e aí vamos conseguir ver melhor onde a função é derivável.Lembrando que para uma função ser derivável ela não pode ter quinas e precisa ser contínua.
Passo 2
Devemos ver em que intervalos a função está “fragmentada”.
Vamos começar olhando para os pontos onde os valores no interior dos módulos zera, que são e :
E como ela se comporta dentro desse intervalo?
Vamos ver alguns valores, tipo , , e ver o que obtemos:
Tudo indica que para valores dentro do intervalo e a função retorna o valor constante .
Passo 3
E para valores fora desse intervalo. Vamos verificar e .
Opa, parece que fora do intervalo a função se comporta de forma simétrica. Como uma reta crescente e de inclinação , pois um acréscimo de duas unidades em representa um acréscimo de 2 unidades em .
Passo 4
Vamos organizar tudo numa tabelinha?
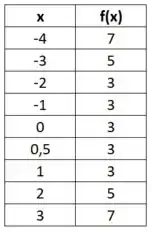
Olhando para a tabela, o que a gente percebe?
A gente percebe que a função é constante e vale para valores entre e .E a gente tem um cheiro de que essa função cresce de forma linear para valores fora desse intervalo.
Fazendo um gráfico teremos:
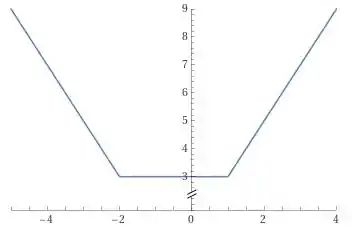
Passo 5
Sobre a derivada do gráfico acima, quando ele é um valor constante a derivada é zero, logo podemos dizer que:
Quando ele se comporta como uma reta, temos que a derivada é a inclinação da reta. A gente avaliou que a inclinação é em módulo igual a dois, pois andar uma unidade em representa uma variação de duas unidades em .
Sendo que a derivada é negativa para , pois a reta é decrescente e positiva para , pois a reta é crescente, logo:
E a função não é diferenciável em e , pois nesses pontos temos quinas.
Por fim, podemos fazer um gráfico para .
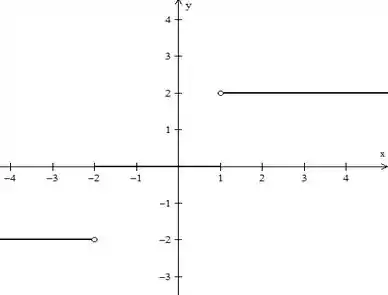
Resposta
A função é derivável para qualquer valor de pertencente aos Reais, exceto para e .
Função :
Gráfico de
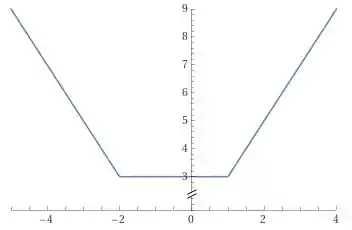
Gráfico de
