Encontre a área da superfície.
A parte do plano que está dentro do cilindro .
Passo 1
Fala, galera! 😉
Precisamos encontrar a área da superfície que está definido pelo plano
Dentro do cilindro
Podemos ver essa superfície na intersecção dos gráficos:
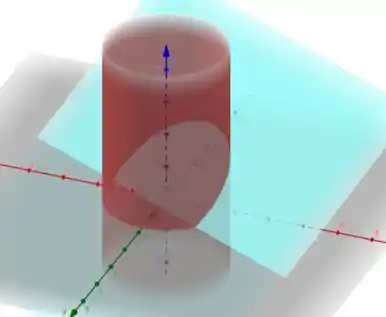
Para resolver, iremos fazer parametrizações e calcular a área de superfície através dessa fórmula aqui:
Onde temos derivadas parciais dentro dessa raiz.
Passo 2
O primeiro passo é encontrar a função para jogarmos dentro da fórmula.
Temos o plano da questão
Isolando o , teremos:
Com isso, vamos fazer as derivadas de em relação a e em relação a :
E os limites de integração? Temos o cilindro de fórmula
Ou seja, no enunciado com
O raio é definido por coordenadas cilíndricas, onde
Passo 3
Agora vamos pra nossa fórmula:
Substituindo todas as informações que temos, chegaremos a
Resolvendo o integrando, com M.M.C., chegaremos a
Podemos jogar a fração para fora da integral e dividir as integrais com seus termos, respectivamente:
Resolvendo cada uma das integrais:
E substituindo pelos limites de integração: