Passe a curva dada para coordenadas polares e desenhe-a:
x4 – y4 = 2xy
Passo 1
Primeiramente, sabemos que:
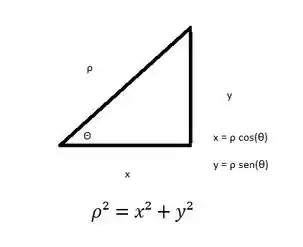
Logo, na primeira parcela:
X4 – y4 = (x² + y²) (x² - y²) = 4 (cos²(
Sabemos que cos²( = cos(, e portanto X4 – y4 = 4 cos(
Passo 2
Do outro lado, temos que 2xy = 2
Sabemos que 2 = sen(2 e portanto, 2xy = 2 = sen(2
Igualando as equações, temos que:
sen(2= 4 cos(
Logo:
Passo 3
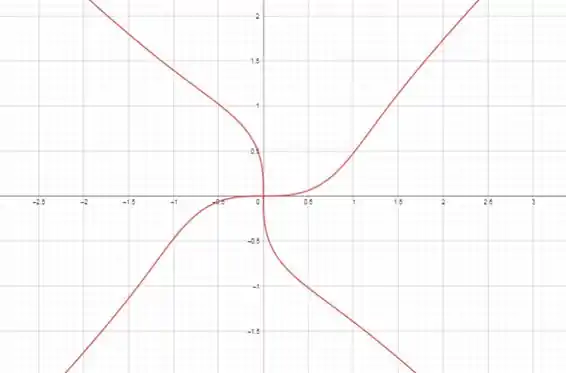
Para esboçar o gráfico, utilizaremos uma tabela de valores que nos ajudará a entender o comportamento da curva:
![]()
Esboçando o gráfico, temos:
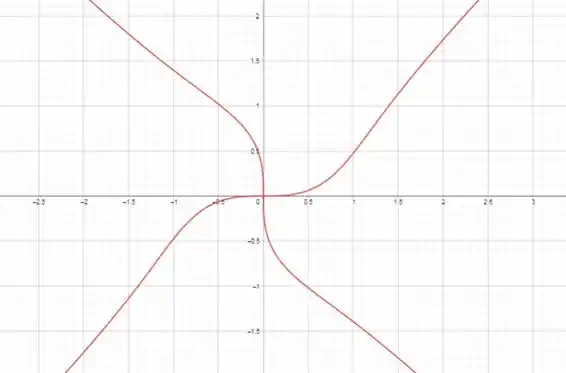
Resposta