O ponteiro dos minutos de um relógio tem de comprimento. Começando do momento em que está apontando diretamente para cima, com que rapidez estará variando a área do setor que é varrido por ele durante uma revolução?
Passo 1
Vamos com calma olhar pro que está acontecendo:
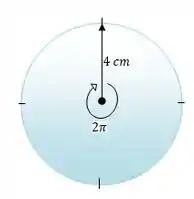
Como podemos relacionar a área varrida com o tempo? Pra isso podemos fazer uma regra de 3, pois sabemos que em , ou seja, a área varrida será a área total do círculo. Então ficaria assim:
Passo 2
Como ele quer a rapidez estará variando a área do setor que é varrido pelo ponteiro durante uma revolução, vamos derivar essa expressão que encontramos:
O raio é o próprio tamanho do ponteiro (), concorda? Então ficamos com: