Resolva as seguintes equações para x ϵ R : a) sen^4 x + cos^4 x = 5 // 8 b) sen^6 x + cos^6 x = 5 // 8 c) sen^4 x + cos^4 x = 1 // 2 d) sen^6 (x)/(2) + cos^6 (x)/(2) = 7 // 16 e) sen^3 x + cos^3 x = 1

a ) x = (pi)/(8) + k pi ; x = (5 pi)/(8) + k pi

Enunciado

Opa galerinha, tudo certo?

Para resolver essa equação vamos relembrar algumas informações importante.

É necessário lembrar do ciclo trigonométrico, como podemos ver abaixo.

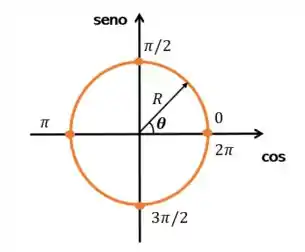
E da relação fundamental da trigonometria:

Simbora! Fazer a questão!

Na letra B temos outro tipo de equação. Dessa vez iremos usar outro método para resolvê-la.

De acordo com a teoria encontrada no livro:

Lembrando da letra A, onde descobrimos um termo equivalente a soma da quarta potência do seno e cosseno.

Para substituir esse produto quadrado de seno e cosseno iremos utilizar mesma lógica desenvolvida na letra A.

Ok! Agora vamos substituir na equação da letra B.

Racionalizando, obtemos:

Então, temos duas possibilidades:

Primeira para um seno positivo.

Esse valor de seno corresponde a de um ângulo notável, no caso, 45 graus.

Segunda para um seno negativo.

Simbora pra letra C!