Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Gelson Iezzi - Fundamentos de Matemática Elementar- Ed: 9º - Capítulo 11.Exercícios - Ex. 327

Determine x tal que sen 3 x + cos 2 x - sen x = 1

Passo 1

Opa galerinha, tudo certo?

Vamos resolver essa equação utilizando a subtração senos e de cossenos e uma relação do cosseno da subtração. Primeiro é importante lembrarmos desses artifícios matemáticos.

A subtração de senos e de cossenos:

sen (w) - sen (v) = 2 * cos ((w + v)/(2)) * sen ((w - v)/(2))

cos (w) - cos (v) = - 2 * sen ((w + v)/(2)) * sen ((w - v)/(2))

E que:

cos ((pi)/(2) - x) = cos (pi)/(2) * cos x + sen (pi)/(2) * sen x = sen x

É importante também lembrar do ciclo trigonométrico, como podemos ver abaixo.

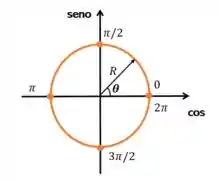
Simbora!

Passo 2

sin 3 x + cos 2 x - sen x = 1

(sen 3 x - sen x) + cos 2 x - 1 = 0

(s e n 3 x - sen x) + ( cos 2 x - cos 0 ) = 0

Utilizando a soma dos senos, onde: {[[w = 3 x],[v = x]]) . E vamos aplicar também a subtração dos cossenos, onde: {[[w = 2 x],[v = 0]])

Assim, a equação fica como:

2 * sen x * cos 2 x - 2 * sen^2 x = 0

Colocando o seno em evidência:

2 * sen x ( cos 2 x - sen x ) = 0

Ok! Aqui temos duas opções, um dos termos do produto é zero para que a igualdade seja verdadeira. Assim:

2 * sen x = 0 -> sin x = 0 -> x = k pi

Ou

cos 2 x - sen x = 0 -> cos 2 x = sen x

A carta na manga aqui é utilizar a seguinte substituição:

sen x = cos ((pi)/(2) - x)

Assim:

cos 2 x = sen x

cos 2 x = cos ((pi)/(2) - x)

2 x = ((pi)/(2) - x) + 2 k pi

x = (pi)/(6) + (2 k pi)/(3)

Resposta

x = (pi)/(6) + (2 k pi)/(3)

Exercícios de Livros Relacionados

Resolva a equação sen^2 x + sen^4 x + sen^6 x = 3
Resolva no conjunto dos números reais a equação sen 2 x = 1 - cos 2 x
Resolva o sistema {[[s e n (x + y) = 0],[x - y = pi]])
Resolva a equação cotg x - sen 2 x = 0
Resolva a equação sin (x + (pi)/(4)) - sin (x - (pi)/(4)) = sqrt(2)