Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 5.11 - Ex. 5

Sabendo que a densidade em cada ponto de um sólido W é dada por f x ,   y ,   z = 1 x 2 + y 2 + z 2 , determine a massa de W quando

W = x ,   y ,   z ∈ R 3   |   x 2 + y 2 + z 2 ≤ 9   e   x 2 + y 2 + z 2 ≥ 2 y

Passo 1

E aí, galerinha!! Vamos lá com mais um exercício com o Responde Aí!! :D

Antes de tudo, vamos revisar uma ideia rapidinho!

Sabemos que a densidade ρ de do ponto de um corpo é dada pela razão entre a sua massa m nesse ponto e seu volume V , ou seja:

ρ = m V

Assim, a massa pode ser dada por:

m = ρ V

E a massa total será:

M = ∫ V ρ d V = ∫ ∫ ∫ W ρ d x d y d z

Assim, para o nosso caso, teremos que:

M = ∫ ∫ ∫ W 1 x 2 + y 2 + z 2 d x d y d z

Então, para calcularmos a integral tripla, o primeiro passo é determinar o domínio das variáveis para saber os limites de integração. No entanto, não é simplesmente determinar esses valores.

Se fizermos o esboço da região (mostrado a seguir) conseguimos ver que ela representa a parte entre duas esferas de raios diferentes:

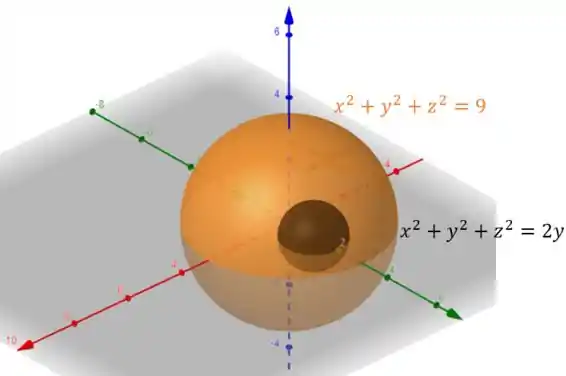
Por conta disso, a massa da região será dada pela subtração entre as massas da esfera maior e da esfera menor. Matematicamente:

M W = M m a i o r - M m e n o r

Como estamos envolvendo superfícies esféricas, no item i i ) da seção 5.10.1 (livro DIOMARA - CÁLCULO DIFERENCIAL E INTEGRAL DE FUNÇÕES DE VÁRIAS VARIÁVEIS - 1 ª ED.) temos que a substituição das variáveis x ,   y ,   z serão dadas por:

x = ρ s e n φ cos ⁡ θ

y = ρ s e n φ s e n θ

E:

z = ρ cos ⁡ φ

Assim, vamos só fazer um cálculo rapidinho. Como todas as equações envolvem o termo x 2 + y 2 + z 2 , se reescrevermos em coordenadas esféricas, teremos:

x 2 + y 2 + z 2 = ρ 2 s e n 2 φ cos 2 ⁡ θ + ρ 2 s e n 2 φ s e n 2 θ + ρ 2 cos 2 ⁡ φ

Juntando os termos semelhantes:

= ρ 2 s e n 2 φ cos 2 ⁡ θ + s e n 2 θ + ρ 2 cos 2 ⁡ φ

E lembrando da identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Podemos reescrever:

= ρ 2 s e n 2 φ + ρ 2 cos 2 ⁡ φ

Tal que:

⇒ ρ 2 s e n 2 φ + cos 2 ⁡ φ = ρ 2

E a nossa integral será dada por:

∫ ∫ ∫ Q 1 ρ 2 ∂ x ,   y ,   z ∂ ρ ,   θ ,   φ d ρ d θ d φ

Onde:

Q = ρ ,   θ ,   φ ∈ R 3   |   ρ ≥ 0 ,     θ 0 ≤ θ ≤ θ 0 + 2 π ,     0 ≤ φ ≤ π

Observando o nosso esboço e seguindo o esquema das coordenadas esféricas para um ponto:

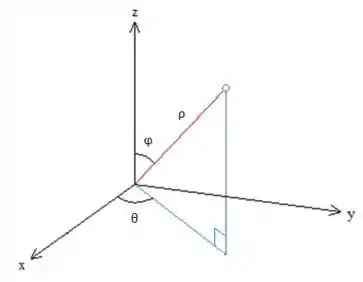
Temos que, para a esfera maior:

0 ≤ θ ≤ 2 π

E:

0 ≤ φ ≤ π

Enquanto que para a esfera menor:

0 ≤ θ ≤ π

E:

0 ≤ φ ≤ π

Ainda, precisamos determinar o módulo do Jacobiano. Então:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = s e n φ cos ⁡ θ - ρ s e n φ s e n θ ρ cos ⁡ φ cos ⁡ θ s e n φ s e n θ ρ s e n φ cos ⁡ θ ρ cos ⁡ φ s e n θ cos ⁡ φ 0 - ρ s e n φ

Isso resulta em:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n 3 φ cos 2 ⁡ θ - ρ 2 s e n φ cos 2 ⁡ φ s e n 2 θ

- ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ - ρ 2 s e n 3 φ s e n 2 θ

Juntando os termos semelhantes, podemos escrever:

⇒ - ρ 2 s e n 3 φ cos 2 ⁡ θ + s e n 2 θ - ρ 2 s e n φ cos 2 ⁡ φ cos 2 ⁡ θ + s e n 2 θ

Usando a identidade trigonométrica:

cos 2 ⁡ u + s e n 2 u = 1

Teremos:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n 3 φ - ρ 2 s e n φ cos 2 ⁡ φ

Ou ainda:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n φ s e n 2 φ + cos 2 ⁡ φ = - ρ 2 s e n φ

Portanto, o módulo do jacobiano é:

∂ x ,   y ,   z ∂ ρ ,   θ ,   φ = - ρ 2 s e n φ = ρ 2 s e n φ

Dessa forma:

⇒ ∫ ∫ ∫ Q 1 ρ 2 ρ 2 s e n φ d ρ d θ d φ

Isso nos dá:

  M = ∫ ∫ ∫ Q s e n φ d ρ d θ d φ

Passo 2

Agora, precisamos determinar os valores que serão os intervalos de cada variável. Para isso, vamos fazer as substituições na equação das esferas. Então, para a maior:

x 2 + y 2 + z 2 = 9

Isso resulta em:

ρ 2 = 9 → ρ = ± 3

Como ρ é positivo, então iremos assumir:

ρ = 3

E, assim:

0 ≤ ρ ≤ 3

Já para a esfera menor:

x 2 + y 2 + z 2 = 2 y

Tal que:

ρ 2 = 2 ρ s e n φ s e n θ

Ou seja:

ρ = 2 s e n φ s e n θ

Portanto:

0 ≤ ρ ≤ 2 s e n φ s e n θ

Passo 3

Com todos esses resultados obtidos, vamos ao cálculo das massas de cada um dos corpos. Primeiro, para a esfera maior:

M m a i o r = ∫ 0 π ∫ 0 2 π ∫ 0 3 s e n φ d ρ d θ d φ

Ou ainda:

⇒ ∫ 0 π s e n φ ∫ 0 2 π ∫ 0 3 d ρ d θ d φ

Então, resolvendo a primeira integral:

= ∫ 0 π s e n φ ∫ 0 2 π ρ | 3 0 d θ d φ

E substituindo o intervalo de integração:

⇒ ∫ 0 π s e n φ ∫ 0 2 π 3 - 0 d θ d φ

= 3 ∫ 0 π s e n φ ∫ 0 2 π 1 d θ d φ

Passo 4

A segunda integral pode ser resolvida por:

3 ∫ 0 π s e n φ ∫ 0 2 π 1 d θ d φ = 3 ∫ 0 π s e n φ θ | 2 π 0 d φ

Substituindo os limites de integração:

⇒ 3 ∫ 0 π s e n φ 2 π - 0 d φ

Teremos:

⇒ 6 π ∫ 0 π s e n φ d φ

Passo 5

Por último, teremos:

6 π ∫ 0 π s e n φ d φ = 6 π - cos ⁡ φ | π 0

E substituindo os limites de integração:

⇒ 6 π - cos ⁡ π - cos ⁡ 0

Portanto:

⇒ M m a i o r = 6 π - - 1 - 1 = 12 π

Passo 6

Agora para a esfera menor:

M m e n o r = ∫ 0 π ∫ 0 π ∫ 0 2 s e n φ s e n θ s e n φ d ρ d θ d φ

Ou ainda:

⇒ ∫ 0 π s e n φ ∫ 0 π ∫ 0 2 s e n φ s e n θ d ρ d θ d φ

Então, resolvendo a primeira integral:

= ∫ 0 π s e n φ ∫ 0 π ρ | 2 s e n φ s e n θ 0 d θ d φ

E substituindo o intervalo de integração:

⇒ ∫ 0 π s e n φ ∫ 0 π 2 s e n φ s e n θ - 0 d θ d φ

= 2 ∫ 0 π s e n 2 φ ∫ 0 π s e n θ d θ d φ

Passo 7

A segunda integral pode ser resolvida por:

2 ∫ 0 π s e n 2 φ ∫ 0 π s e n θ d θ d φ = 2 ∫ 0 π s e n 2 φ - cos ⁡ θ | π 0 d φ

Substituindo os limites de integração:

⇒ 2 ∫ 0 π s e n 2 φ - cos ⁡ π - cos ⁡ 0 d φ

Teremos:

⇒ 2 ∫ 0 π s e n 2 φ - - 1 - 1 d φ = 4 ∫ 0 π s e n 2 φ d φ

Passo 8

Por fim, podemos aplicar a identidade trigonométrica:

s e n 2 u = 1 - cos ⁡ 2 u 2

Para resolver a integral. Dessa forma, ela será escrita como:

4 ∫ 0 π s e n 2 φ d φ = 4 ∫ 0 π 1 - cos ⁡ 2 φ 2 d φ

Isso pode ser reescrito como:

2 ∫ 0 π 1 - cos ⁡ 2 φ d φ

Logo:

2 ∫ 0 π 1 - cos ⁡ 2 φ d φ = 2 φ - s e n 2 φ | π 0

E substituindo os limites de integração:

⇒ 2 π - s e n 2 π - 0

Portanto:

⇒ M m e n o r = 2 π

Passo 9

Então, é possível concluir que a massa da região W terá o resultado:

M W = M m a i o r - M m e n o r

M W = 12 π - 2 π = 10 π

Resposta

10 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o centro de massa do tetraedro sólido com vértices ( 0 ,0 ,0 ) ,( 1 ,0 ,0 ) ,( 0 ,2 ,0 ) ,( 0 ,0 ,3 ) e função densidade ρ x , y , z = x 2 + y 2 + z 2 .
Encontre o centro de massa e o momento de inercia em relação ao plano y de uma placa fina delimitada pelo eixo x, pelas retas x = ± 1 , e pela parábola y = x 2 se d e l t a x , y = 7 y + 1 .
Encontrando o momento de inercia: encontre o momento de inercia em relação ao eixo y de uma folha fina de densidade constante δ = 1 delimitada pelas curvas y = s e n 2 x x 2 e o intervalo π ≤ x ≤ 2 π
Primeiro momento de uma placa infinita: encontre o primeiro momento de inercia em relação ao eixo y de uma placa fina de densidade δ x , y = 1 que cobre a rgião infinita sob a curva y = e - x 2 2 no p
Encontrando momentos de inercia: encontre os momentos de inercia em relação aos eixos coordenados de uma placa fina retangular de densidade constante δ delimitada pelas curvas x = 3 e y = 3 no primeir