Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.3 - Ex. 54

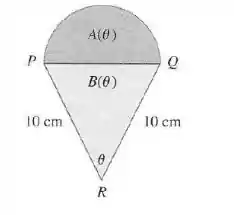
O semicírculo com diâmetro P Q está sobre um triangulo isósceles P Q R para formar uma região com um formato de sorvete, conforme mostra a figura. Se A ( θ ) for a área do semicírculo e B ( θ ) a área do triângulo, encontre

lim θ → 0 + ⁡ A ( θ ) B ( θ )

Passo 1

Olá, amigo, Yuri aqui e agora eu e você iremos resolver essa atividade.

A atividade nos pede para encontrarmos primeiramente a área do triangulo e do semicírculo do nosso ‘sorvete’ e após isso calcular o limite de seu consciente.

A área de um triangulo é dada por:

A   =   B ∙ H 2

E a área de uma semicircunferência:

A   =   π r 2 2

Então primeiramente, devemos relacionar A ( θ ) e B ( θ ) com θ .

Veja só!

Passo 2

A ( θ ) é a área do semicírculo cujo raio é a metade do segmento P Q :

A θ = π P Q 2 2 2

O segmento P Q tem o comprimento de:

sen ⁡ θ 2 = P Q 2 10

P Q = 20 sen ⁡ θ 2

Então o raio do semicírculo fica:

P Q 2 = 10 sen ⁡ θ 2

E área vai ser:

A θ = π 10 sen ⁡ θ 2 2 2

A θ = π 100 sen 2 ⁡ θ 2 2

A θ = 50 π sen 2 ⁡ θ 2

Tranquilo até aqui?

Passo 3

B ( θ ) é a área do triângulo cuja altura h é a distância do ponto R até o ponto médio do segmento P Q :

B θ = P Q × h 2

A altura desse triângulo vai ser:

Então a área fica assim:

B θ = 20 sen ⁡ θ 2 × 10 cos ⁡ θ 2 2

B θ = 100 sen ⁡ θ 2 cos ⁡ θ 2

Show?

Passo 4

Então, a razão entre as áreas é:

A θ B θ = 50 π sen 2 ⁡ θ 2 100 sen ⁡ θ 2 cos ⁡ θ 2

A θ B θ = π sen ⁡ θ 2 2 cos ⁡ θ 2

A θ B θ = π 2 tg ⁡ θ 2

Logo:

lim θ → 0 + ⁡ A θ B θ = lim θ → 0 + ⁡ π 2 tg ⁡ θ 2 = π 2 lim θ → 0 + ⁡ tg ⁡ θ 2

lim θ → 0 + ⁡ A θ B θ = π 2 · tg ⁡ 0

lim θ → 0 + ⁡ A θ B θ = 0

E aí! o que achou? Responde Aí!

Resposta

lim θ → 0 + ⁡ A θ B θ = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f x = s e nx . Encontre todos os inteiros positivos n com os quais f n x = s e nx .
Use o Método de Newton para aproximar a menor solução positiva de sen ⁡ x + cos ⁡ x = 0 .
30-a) Use recurso gráfico para fazer estimativas rudimentares dos pontos no intervalo [ 0,2 π ] nos quais o gráfico de y = s e nx cos ⁡ x tem uma reta tangente horizontal.b) Encontre a exata localizaç
Em cada parte, explique o que acontece se aplicarmos o Método de Newton a uma função f quando a condição dada é satisfeita para algum valor de n . f x n = 0 x n + 1 = x n x n + 2 = x n ≠ x n + 1
Encontre f^' (x) . f (x) = ((x^2 + 1) c o t g x)/(3 - cos x c o s s e c x)