Suponha que , e e para todo .
(a) Esboce um gráfico possível de .
(b) Quantas soluções a equação tem? Por quê?
(c) É possível que ? Por quê?
Passo 1
Fala aí, galerinha!
Nesse problema foram dadas algumas informações de uma função e nosso objetivo é, a partir dessas informações, esboçar um possível gráfico de , determinar quantas raízes têm e se é possivel ter .
Parece complicado?
Para resolver esse problema vamos analisar cada uma das informações dadas e discutir como elas se relacionam com o gráfico da função.
E a partir do seu gráfico, vamos responder quantas possíveis soluções temos e se é possivel termos .
Partiu?
Passo 2
Se então o ponto pertence ao gráfico de .
Como para qualquer valor de , então é crescente em todo o seu domínio e já que a função possui concavidade voltada para baixo para todo .
Além disso, em , temos que , então a inclinação da reta tangente a nesse ponto é .
A partir desses dados o gráfico pode ser esboçado por:
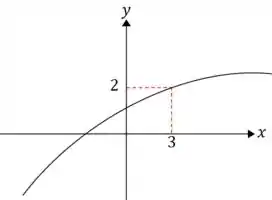
Tranquilo até aqui?
Passo 3
No item b) o problema pergunta quantas soluções podemos ter...
Como vimos no passo anterior, só existe apenas uma solução pois é crescente em todo seu domínio, logo seu gráfico só corta o uma única vez.
Bacana, não é?
Passo 4
E no item c) o problema pergunta se é possivel que ...
Se a derivada segunda é sempre negativa, então a derivada primeira é sempre decrescente. Desse modo, se tivermos um número maior que um número () a derivada aplicada no menor é maior que a derivada aplicada no maior, ou seja:
Logo, se e então:
Como não é maior que então não é um valor possível para .
E fim! O que achou? Responde Aí!
Resposta
(a)
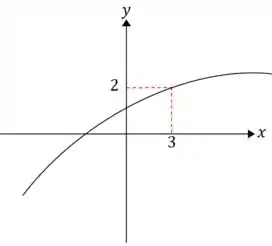
(b) Só existe apenas uma solução .
(c) então não é um valor possível para .