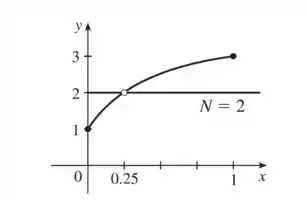
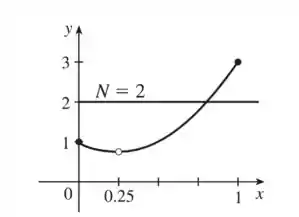
Suponha que uma função seja contínua em , exceto em , e que e . Seja . Esboce dois gráficos possíveis de , um indicando que pode não satisfazer a conclusão do Teorema do Valor Intermediário e outro mostrando que Poderia ainda satisfazer a conclusão do Teorema Valor Intermediário (mesmo que não satisfaça as hipóteses).
Passo 1
Opa! Galera, nessa questão devemos elaborar dois gráficos para a questão com as seguintes condições:
Ela deve ser contínua em
Ela deve ser desconcontínua em
No primeiro gráfico a gente deve ter a curva de uma função que não obedece a conclusão do Teorema do Valor Intermediário e no segundo ela deve obedecer! Esse teorema diz que:
“Se for uma função contínua em um intervalo fechado e um número qualquer entre e , em que . Então existe um número em tal que .”
Temos que:
De fato temos que esta entre e .
Em um gráfico devemos ter uma descontinuidade em e assim ele não vai respeitar a conclusão do Teorema do valor intermediário, porque não vai existir um valor em tal que . No outro a descontinuidade vai ser em qualquer valor de entre e que seja diferente de . Sacou?!
Passo 2
Agora é só desenhar, respeitando os pontos conhecidos:
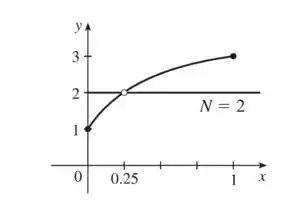
Repara que não existe um valor em tal que , pois no ponto onde deveríamos ter a função é descontinua!
Passo 3
Vamos para o segundo gráfico:
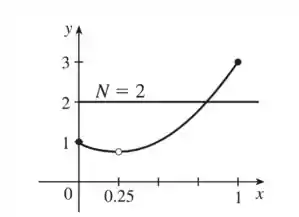
Aqui temos um , não conhecemos esse mas podemos ver que ele existe!
Resposta