Exercícios de Teorema do Valor Intermediário - Lista de Exercícios Resolvida
Questão 1
Seja uma função contínua em ℝ tal que e , e seja . A função composta possui duas raízes negativas distintas. Determine intervalos abertos disjuntos contendo cada uma dessas raízes.
Ver solução completaQuestão 2
A partir dos gráficos abaixo, justifique, se para cada função:
- A tese do Teorema do Valor Intermediário é satisfeita.
- A hipótese Teorema do Valor Intermediário é satisfeita.
Obs: A tese pode ser interpretada como o “resultado” de um teorema. A hipótese pode ser interpretada como a “condição” para que o teorema funcione.
a):
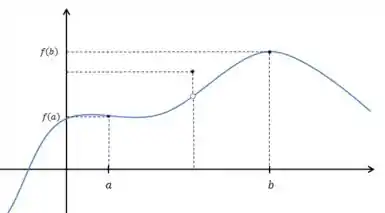
b):
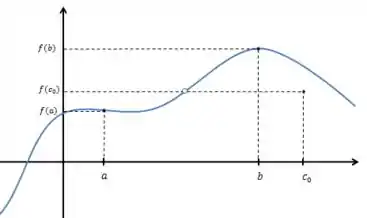
c):
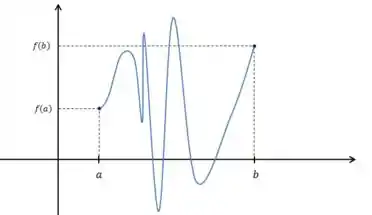
Questão 3
Dê um exemplo de uma função tal que em dois pontos distintos , a função tenha sinais contrários, f não é contínua no intervalo e
a tese do Teorema do Valor Intermediário é verdadeira.
a tese do Teorema do Valor Intermediário é falsa.
Ver solução completaQuestão 4
Mostre que os gráficos de e têm interseção em pelo menos um ponto do intervalo
Ver solução completaQuestão 5
Determine um intervalo de amplitude 1, no qual está localizado pelo menos um zero dessa função.
Ver solução completaQuestão 7
Considere a função dada por
Mostre que existe tal que . (Dica: Use o Teorema do Valor Intermediário).
Ver solução completaQuestão 8
Utilizando o Teorema do Valor Intermediário (TVI) justifique que a equação
possui uma solução não nula.
Ver solução completaQuestão 9
Questão 1.1: Seja uma função contínua tal que , , , e . Considere as seguintes afirmações:
(a) A reta se intersepta com o gráfico de exatamente vezes.
(b) A reta se intersepta com o gráfico de pelo menos vezes.
(c) A reta se intersepta apenas uma vez com o gráfico de .
(d) A reta não se intersepta com o gráfico de .
Ver solução completaQuestão 10
Sejam e dadas por
Onde e são constantes reais positivas.
Prove que tem pelo menos uma raiz no intervalo .
Ver solução completaQuestão 11
24) Determine um intervalo de amplitude 1, no qual está localizado pelo menos um zero dessa função.
Ver solução completaQuestão 12
Dê um exemplo de uma função tal que em dois pontos distintos e a função tem sinais contrários, não é contínua no intervalo e a tese do Teorema do Valor Intermediário é verdadeira.
Ver solução completaQuestão 13
Considere as alternativas abaixo:
- Se é contínua em e e então, pelo Teorema do Valor Intermediário, para todo no intervalo .
- Se é contínua no intervalo e , então existe tal que .
É verdadeira ou são verdadeiras:
- Somente a afirmativa (II)
- Nenhuma das afirmativas.
- Somente a afirmativa (I).
- As afirmativas (I) e (II).
Questão 16
Nos modelos de queda livre, costuma-se supor que a aceleração da gravidade na superfície da terra é constante igual a 9,8 m/s². Na verdade, g é função da latitude que, medida em graus, é dada pela seguinte fórmula:
Mostre que existe um tal que
Ver solução completaQuestão 17
23- Prove que a equação possui uma solução no intervalo , onde é a constante de Euler.
Ver solução completaQuestão 20
Mostre que a função
assume o valor no intervalo .
Dica: Use o Teorema do Valor Intermediário (TVI).
Ver solução completaQuestão 21
Sobre a equação , é correto afirmar:
- Admite solução no intervalo .
- Não admite solução real.
- Admite solução no intervalo .
- Admite solução no intervalo
- Admite solução no intervalo .
Questão 22
Mostre que os gráficos de e tem interseção em pelo menos um ponto do intervalo .
Ver solução completaQuestão 23
Questão 4:
Use o teorema do valor intermediário (TVI) para mostrar que a equação tem uma solução no .
Ver solução completaQuestão 25
Seja a função . Determine os valores de que satisfaz o Teorema do Valor Médio.
Ver solução completaQuestão 26
Use o Teorema do Valor intermediário para mostrar que a equação tem uma solução no intervalo .
Ver solução completaQuestão 27
Use o Teorema do Valor Intermediário (TVI) para mostrar que a equação
tem pelo menos uma raiz real.
Ver solução completaQuestão 28
Use o Teorema do Valor Intermediário (TVI) para mostrar que a equação
possui uma solução positiva.
Ver solução completaQuestão 29
5. Seja uma função contínua que satisfaz , e . Para qual dos valores abaixo a equação possui, com certeza, pelo menos duas raízes reais distintas.
Questão 30
28) Dê um exemplo de uma função tal que em dois pontos distintos e a função tem sinais contrários, não é contínua no intervalo e a tese do Teorema do Valor Intermediário é verdadeira.
Ver solução completaQuestão 31
Um monge tibetano deixa o monastério às 7 horas da manha e segue sua caminhada
usual ate o topo da montanha, chegando lá as 7 horas da noite. Na manhã seguinte ele parte
do topo as 7 horas da manha e, andando pelo mesmo caminho, chega no monastério as 7
horas da noite. Mostre que existe um ponto no caminho que o monge vai cruzar exatamente
na mesma hora do dia em ambas caminhadas.
Ver solução completaQuestão 32
Seja uma função contínua no intervalo e suponha que e possuam sinais opostos. Sabemos pelo Teorema do Anulamento que possui pelo menos uma raiz no intervalo . Descubra uma estratégia que possa ser implementada em um computador para encontrar essa raiz.
Ver solução completaQuestão 33
26) Determine um intervalo de amplitude 1, no qual está localizado pelo menos um zero dessa função.
Ver solução completaQuestão 34
27) Mostre que os gráficos de e têm intersecção em pelo menos um ponto do intervalo .
Ver solução completaQuestão 35
30) Se uma função muda de sinal quando varia de um ponto para o ponto , existirá obrigatoriamente um ponto entre e onde a função se anula? Justifique sua resposta.
Ver solução completaQuestão 36
25) Determine um intervalo de amplitude 1, no qual está localizado pelo menos um zero dessa função.
Ver solução completaQuestão 37
29) Dê um exemplo de uma função tal que em dois pontos distintos e tem sinais contrários, não é contínua no intervalo e a tese do Teorema do Valor Intermediário é falsa.
Ver solução completaQuestão 38
Dados e o intervalo fechado . Usando o Teorema do Valor Intermediário mostre que existe pelo menos um valor entre e tal que .
Ver solução completaQuestão 39
A equação
não tem raízes reais.
tem pelo menos três raízes reais.
: tem exatamente uma raiz real negativa, mas não tem uma raiz real positiva.
tem exatamente uma raiz real positiva, mas não tem uma raiz real negativa.
tem exatamente duas raízes reais.
Ver solução completaQuestão 41
Se e são números positivos, prove que a equação abaixo possui no mínimo uma solução no intervalo (-1, 1)
Ver solução completaQuestão 42
Seja um intervalo. Mostre que se é uma função contínua que não se anula no intervalo então ou para todo ou para todo .
Ver solução completaQuestão 43
A temperatura T (em °C) na qual a água ferve é dada aproximadamente pela fórmula
Onde h é a altitude (em metros acima do nível do mar). Mostre que a água ferve a 98°C a uma altitude entre 4000 e 4500 metros.
Ver solução completaQuestão 44
Se uma função muda de sinal quando varia de um ponto para o ponto , existirá obrigatoriamente um ponto entre e onde a função f se anula? Justifique sua resposta.
Ver solução completaQuestão 45
5. Use o teorema do valor intermediário para mostrar que a equação
Possui pelo menos uma solução real.
Ver solução completaQuestão 46
3. Uma função satisfaz as seguintes propriedades:
- e
- é estritamente crescente em e
- é uma função par
d. Supondo que seja contínua no intervalo , ela teria alguma raiz nesse intervalo? Justifique.
Ver solução completaQuestão 47
Faça o que se pede:
Use o Teorema do Valor Intermediário (TVI) para mostrar que a equação
Possui ao menos uma solução não-nula.
Ver solução completaQuestão 48
Use o Teorema do Valor Intermediário para mostrar que a equação
Tem pelo menos uma raiz no intervalo
Ver solução completaQuestão 49
Use o Teorema do Valor Intermediário (TVI) para mostrar que a equaç ao
tem uma solução no intervalo
Ver solução completaQuestão 50
Seja a função
Use o Teorema do Valor Intermediário para mostrar que a equação admite
ao menos três soluções reais.
Ver solução completaQuestão 51
Seja , onde e são dados. Calcule os limites no infinito e, em seguida, use o Teorema do Valor Intermediário para mostrar que possui pelo menos uma raiz. O que se pode dizer se ?
Ver solução completaQuestão 52
Use o TVI para mostrar que a equação
possui pelo menos duas soluções. Estime estas soluções com casas decimais.
Ver solução completaQuestão 53
Determine:
Um intervalo de comprimento igual a que contém uma raiz de
Ver solução completaQuestão 54
Usando o Teorema do Valor Intermediário, mostre que a equação
Possui uma raiz no intervalo
Ver solução completaQuestão 55
4. Mostre que a função possui, pelo menos, uma raiz real no intervalo .
Ver solução completaQuestão 56
7.17. Use o TVM para provar as seguintes desigualdades:
(a) , para todos .
Ver solução completaQuestão 57
7.18. Seja uma função derivável no intervalo tal que e , para todo . Mostre que , para todos .
Ver solução completaQuestão 58
7.17. Use o TVM para provar as seguintes desigualdades:
(c) , para todos , com e .
Ver solução completaQuestão 59
7.17. Use o TVM para provar as seguintes desigualdades:
(d) , para todos , com .
Ver solução completaQuestão 60
7.17. Use o TVM para provar as seguintes desigualdades:
(f) , para todos com .
Ver solução completaQuestão 61
7.17. Use o TVM para provar as seguintes desigualdades:
(b) , para todos , com e .
Ver solução completaQuestão 62
7.17. Use o TVM para provar as seguintes desigualdades:
(e) , para todos , com .
Ver solução completaQuestão 67
Sejam o círculo de raio e centro em e , o círculo de raio , , e centro em . Sejam ainda o ponto e o ponto de intersecção dos círculos e situado no primeiro quadrante.
Se é a intersecção da reta com o eixo , o que acontecerá com , quando encolher arbitrariamente?
Ver solução completaQuestão 69
C3. A função satisfaz e , isto é, e possuem sinais opostos. É possível usar o Teorema do Anulamento para concluir que possui uma raiz no intervalo (−1, 1)?
Ver solução completaQuestão 70
Determine um intervalo de amplitude , no qual está localizado pelo menos um zero da função.
Ver solução completaQuestão 71
Q05) Use o teorema do valor intermediário (TVI) para mostrar que a equação
Tem uma solução no intervalo . Relembre que
Ver solução completaQuestão 72
Verifique que a equação possui pelo menos alguma solução para um positivo.
Ver solução completaQuestão 73
C2. Classifique cada item abaixo como verdadeiro ou falso.
a) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
b) Pelo Teorema do Valor Intermediário, é possível concluir que a função
possui pelo menos uma raiz real no intervalo .
c) Seja . Pelo Teorema do Valor Intermediário, é possível concluir que existe ∈ [0,4] tal que .
d) A função possui, pelo menos, uma raiz real.
e) Toda função contínua possui, pelo menos, uma raiz real.
Ver solução completaQuestão 74
Dê um exemplo de uma função tal que em dois pontos distintos e a função tem sinais contrários, não é contínua no intervalo e a tese do Teorema do Valor Intermediário é falsa.
Ver solução completa