Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.7 - Ex. 48

A temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola. Determine a taxa de transmissão de calor através de uma esfera S de raio a e centro da bola.

Passo 1

Oi galera, tudo bem?

Precisamos encontrar a taxa de transmissão de calor através de uma esfera de raio a . Sabendo que a temperatura de um ponto da bola com condutividade K é inversamente proporcional à distância do centro da bola.

Vamos com calma!!!

Pra calcular a taxa de transmissão de calor Φ vamos relembrar como é a fórmula:

Φ = ∬ S K ∇ → u ⋅ d S →

Onde,

K é a condutividade.

∇ → u é o gradiente da condutividade térmica.

d S → = n →   d A

Então, aqui temos de considerar uma esfera de raio a centrada na origem.

x 2 + y 2 + z 2 = a 2

Podemos escrever um vetor normal à esfera que aponta para fora da seguinte forma:

n → = 1 a ( x i → + y j → + z k → )

E como ele falou que a condutividade é inversamente proporcional à distância da bola, podemos escrever:

u = c x 2 + y 2 + x 2

Observe que já temos todas as informações, agora é substituir na integral e fazer o produto escalar.

Lembre-se que em coordenadas esféricas temos:

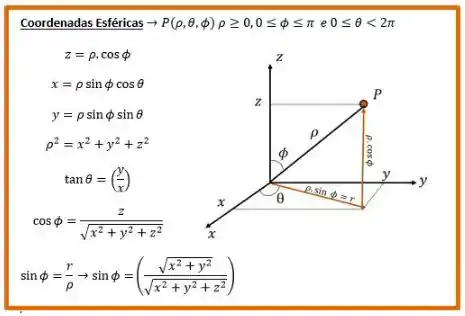
O diferencial de área vai ser d A = r 2 s e n θ   d θ d ϕ entre os limites:

0 ≤ ϕ ≤ π 0 ≤ θ ≤ 2 π

Bora lá resolver!

Passo 2

Vamos começar determinando o gradiente da condutividade.

u = c x 2 + y 2 + x 2

Lembre-se que o gradiente fornece um vetor, ele é:

∇ → u = d u d x i → + d u d y j → + d u d z k →

Sendo assim o valor de ∇ → u é:

∇ → u = c x 2 + y 2 + z 2 3 2 ( x i → + y j → + z k → )

Agora podemos substituir na integral.

Lembrando que d S → é:

d S → = �� n → d A = 1 a x i → + y j → + z k →   d A

Ficando assim:

Φ = ∬ S K c x 2 + y 2 + z 2 3 2 x i → + y j → + z k → ⋅ 1 a x i → + y j → + z k →   d A

Aplicando o produto escalar, vamos ter:

Φ = ∬ S c K a x 2 + y 2 + z 2 x 2 + y 2 + z 2 3 2 d A

Repare que podemos simplificar ainda mais, ficando:

Φ = ∬ S c K a 1 x 2 + y 2 + z 2 1 2   d A

Repare que podemos substituir x 2 + y 2 + z 2 1 2 por a . Por que isso? Porque ele nos forneceu no enunciado que a expressão da esfera é:

x 2 + y 2 + z 2 = a 2

Logo, nossa integral fica:

Φ = ∬ S c K a 2   d A

Passo 3

Sabemos que o diferencial de área é:

d A = r 2 s e n θ d θ d ϕ

E os limites de integração varia entre:

0 ≤ ϕ ≤ π 0 ≤ θ ≤ 2 π

Agora vamos colocar tudo na integral:

Φ = ∬ S c K a 2   d A

Ficando assim:

Φ = c K a 2 ∫ 0 2 π ∫ 0 π a 2   s e n ϕ d ϕ d θ

Simplificando um pouco, temos:

Φ = c K ∫ 0 2 π ∫ 0 π   s e n ϕ d ϕ d θ

Agora, precisamos começar a integral. Começando integrando em d ϕ , vamos ter:

Φ = c K ∫ 0 2 π - c o s ϕ 0 π   d θ

Substituindo os limites de integração, ficamos com:

Φ = c K ∫ 0 2 π - - 1 - 1 d θ   d θ

Φ = 2 c K ∫ 0 2 π d θ

Por fim, ficamos com uma integral simples em d θ . Integrando, temos:

Φ = 2 c K θ 0 2 π

Aplicando os limites de integração vamos obter a seguinte resposta:

Φ = 4 K c π

Observe também, que a taxa de transmissão de calor Φ independe do raio a da esfera.

Resposta

Φ = 4 K c π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 . prove que Se a superficie S é dada na forma explicita por y = yx , z ,x , z ∈ R ' , onde R’ é a projeção sobre o plano xz e n denota a normal unitária de S com a componente y não negativa, obtemos
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( x , y , - 2 z ) e S é a esfera x 2 + y 2 + z 2 = 4 , com vetor normal n exterior.
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( z 2 - x , - x y , 3 z ) e S é a superfície do sólido limitado por z = 4 - y 2 , x = 0 , x = 3 e o plano x y , com vetor normal n exteri
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( x , y , x z ) e S é a superfície do sólido W , onde W = x , y , z ∈ R 3 x 2 + y 2 ≤ z ≤ 1 , com vetor normal n exterior.
Calcule ∬ S F ⋅ n d s nos exercícios abaixo: F ( x , y , z ) = ( x , y , z ) e S é o triângulo de vértices ( 1,0 , 0 ) , ( 0,1 , 0 ) e ( 0,0 , 1 ) , onde o vetor normal n tem componente z não negativa