Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 46d
Traçar o gráfico das funções trigonométricas. Comparar cada conjunto identificando a transformação ocorrida. Identificar domínio, conjunto imagem, máximos e mínimos, crescimento e decrescimento.
d)
Passo 1
Então pessoal, de início vamos plotar o gráfico das funções , e que nos foram dadas, tudo bem? A é uma função cosseno bem conhecida, a é a mesma função deslocada casas para a esquerda e a é a mesma função deslocada casas para a direita. Para confirmarmos:
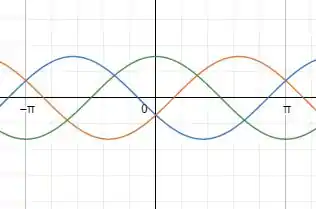
No qual a função em verde é ;
A função em azul é ;
A função em laranja é .
Passo 2
Para facilitar a nossa análise, como são vários pontos para analisar vamos pontuar um de cada vez, tudo bem? Primeiramente temos:
- Transformações ocorridas:
- Domínio:
- Imagem:
- Máximos:
- Mínimos:
- Intervalos de crescimento:
- Intervalos de decrescimento:
Assim como já descrito no passo , de para houve uma translação horizontal para a esquerda, uma vez que há uma soma na variável independente .
De para já ocorre o contrário, o que houve foi uma translação horizontal para a direita, uma vez que há uma subtração na variável independente .
Então galera, todas as três funções possuem o mesmo comportamento, a única coisa que muda é aonde cada uma delas começa no gráfico! Como se tratam de funções periódicas, então podemos assumir qualquer valor para , que é o nosso domínio. Sendo assim, teremos que:
A imagem das funções seno, cosseno e tangente são bem conhecidas, uma vez que se tratam de imagens beeem limitadas! Sabemos que as funções seno e cosseno possuem a mesma imagem, são funções que variam de a , não é mesmo? Sendo assim, teremos:
Passo 3
Agora vamos determinar os máximos e mínimos das funções!
Sabemos que o período da função cosseno é , certo? Ademais, a função cosseno é máxima quando vale , assim como vimos no passo anterior. Dessa forma, para a função :
Para as funções e é praticamente a mesma coisa, a diferença é que há aquelas constantes na variável, então os máximos serão:
E faz sentido, uma vez que se substituirmos esses valores nas funções obteremos pois as constantes sumirão!
De forma contrária aos máximos, a função cosseno é mínima quando vale , assim como vimos no passo anterior. Dessa forma, para a função :
Utilizando o mesmo raciocínio que fizemos para as funções e nos pontos de máximos:
Aqui vale ressaltar que é uma constante inteira, tudo bem?
Passo 4
Por fim, vamos determinar os intervalos de crescimento e decrescimento!
Os intervalos de crescimento ocorrem quando a função está atingindo seu ponto de máximo, que no caso da nossa função é em . Sendo assim, os intervalos serão em:
O raciocínio é exatamente o que utilizamos para determinar os máximos, pessoal!
Os intervalos de decrescimento ocorrem quando a função está atingindo seu ponto de mínimo, que no caso da nossa função é em . Sendo assim, os intervalos serão em:
Que também é o raciocínio que utilizamos para determinar os mínimos, galera! Outra vez vale ressaltar que é um número inteiro, belê? Ufa! Foi demorado, mas está aí nossa análise completa!
Resposta
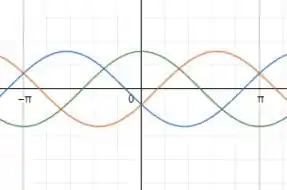
Domínio e imagem:
Máximos e mínimos:
Intervalos de crescimento e decrescimento: