Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 45

Trace a curva e calcule seu comprimento:

x = e t cos ⁡ t ,     y = e t s e n   t   ,   0 ≤ t ≤ π

Passo 1

Falai galerinha. De boa? Preparado para traçar uma curva parametrizada por x = e t cos ⁡ t ,     e y = e t s e n   t no intervalo 0 ≤ t ≤ π e calcular o comprimento dessa curva?

Vamos entender um pouco como faremos isso? Se liga! 😊

Para resolver o problema

  1. Traçamos a curva no plano cartesiano utilizando a parametrização dada.
  2. Em seguida, para calcular o comprimento da curva, utilizamos a fórmula do comprimento de arco para curvas parametrizadas:

    3. L = ∫ a b d x d t 2 + d y d t 2 d t .

  3. Calculamos as derivadas d x d t ​ e d y d t ​ e substituímos na fórmula.
  4. Simplificamos a expressão resultante e integramos numericamente no intervalo dado, obtendo o comprimento aproximado.

Agora é só resolver, Bora!

Passo 2

Primeiro vamos traçar a curva no gráfico, faremos isso escolhendo valores e substituindo nas equações de x e y .

Com ajuda de um programa, temos

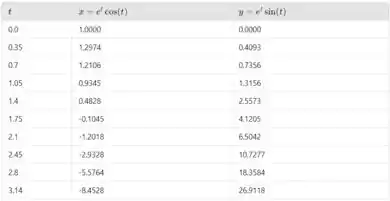
Podemos construir o gráfico

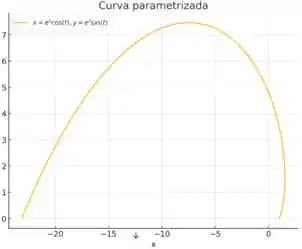
Passo 3

Agora que já temos a fórmula podemos substituir os valores dados, diferenciando x   e   y ,   certo?

Para x

x = e t cos ⁡ t    

Derivando e utilizando a Regra do Produto, temos

d x ' = e t cos ⁡ t -   e t s e n   t   d t

Através de uma manipulação matemática, elevamos os lados ao quadrado.

d x d t 2 = e 2 t cos 2 ⁡ t - 2 e 2 t cos ⁡ t   s e n   t +   e 2 t s e n 2 t  

Para y

y = e t s e n   t

Utilizado a Regra do Produto

d y ' = e t cos ⁡ t +   e t s e n   t   d t

Através de uma manipulação matemática, elevamos os lados ao quadrado.

d y d t 2 = e 2 t cos 2 ⁡ t + 2 e 2 t cos ⁡ t   s e n   t +   e 2 t s e n 2 t  

Passo 4

Só substituir, sem esquecer dos limites de integração né:

L = ∫ 0 π e 2 t cos 2 ⁡ t - 2 e 2 t cos ⁡ t   s e n   t +   e 2 t s e n 2 t + e 2 t cos 2 ⁡ t + 2 e 2 t cos ⁡ t   s e n   t +   e 2 t s e n 2 t   d t  

L = ∫ 0 π e 2 t cos 2 ⁡ t +   e 2 t s e n 2 t + e 2 t cos 2 ⁡ t +   e 2 t s e n 2 t   d t  

L = ∫ 0 π 2 e 2 t cos 2 ⁡ t +   2 e 2 t s e n 2 t   d t  

Como s e n 2 t + cos 2 ⁡ t = 1 :

2 e 2 t s e n 2 t + 2 e 2 t cos 2 ⁡ t = 2 e 2 t

L = ∫ 0 π 2 e t   d t  

L = 2 e t π 0

O comprimento pode ser calculado a partir da equação

L = 2 ( e π - 1 )

Resposta

L = 2 ( e π - 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1. Calcule o comprimento da curva dada:b)gamma (t) = (2 t - 1 , t + 1) , t in [1 , 2]
Calcule o comprimento da curva dada em coordenadas polares (Utilize o exercício 2) c )ρ = sin ⁡ θ , θ ∈ 0 , π
Reparametrize pelo comprimento de arco a curva γ dada: c )γ t = cos ⁡ t , sin ⁡ t ,t , t ≥ 0
Reparametrize pelo comprimento de arco a curva γ dada: b )γ t = cos ⁡ t , sin ⁡ t ,t , t ≥ 0
Dizemos que uma δ : α ,β → R n , com derivada contínua, está parametrizada pelo comprimento de arco se δ ' s = 1 , para todo s ∈ α ,β . Verifique que cada uma das curvas abaixo está parametrizada pelo