Exercícios de Comprimento de Arco - Lista de Exercícios Resolvida

Uma curva tem equação . Encontre o comprimento da curva do ponto ao ponto .

Uma partícula se move ao longo de uma curva definida por

1. Determine os instantes e em que .
2. Calcule o espaço percorrido pela partícula no intervalo de tempo .

Uma partícula se move numa hélice com vetor posição no tempo , Qual é o tempo para que a distância percorrida seja ?

(a)

(b)

(c)

(d)

(e)

Encontre o comprimento do caminho percorrido por uma partícula que se move ao longo da curva de equação dada durante o intervalo de tempo especificado:

Uma curva é a união de duas curvas e , onde é um segmento de reta e é uma porção da circunferência, conforme a figura. Pede-se:

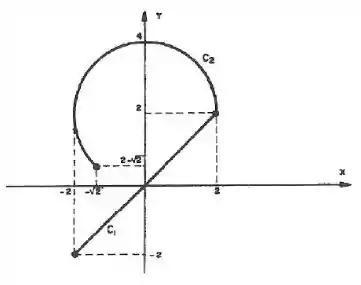
1. Parametrize curvas e
2. O comprimento total de .

16 - Determine o comprimento das curvas:

e) , .

Seja uma partícula cuja posição no espaço ao longo do tempo é descrita pela função vetorial , com .

Calcule o comprimento de arco (distância percorrida pela partícula) entre os tempos e .

Uma partícula se move numa hélice com vetor posição no tempo , Qual é o tempo para que a distância percorrida seja ?

(a)

(b)

(c)

(d)

(e)

(Cap. 13.3 - Ex. 4) Determine o comprimento da curva dada.

16 - Determine o comprimento das curvas:

c) de a .

16 - Determine o comprimento das curvas:

d) de a .

16 - Determine o comprimento das curvas:

b) de a .

16 - Determine o comprimento das curvas:

a) de a .

15 - Determine o comprimento das curvas parametrizadas:

d) , , .

15. Determine o comprimento de arco da curva .

3) Sejam as curvas e Desenhadas em anexo. Formule, em cada caso, uma integral para calcular:

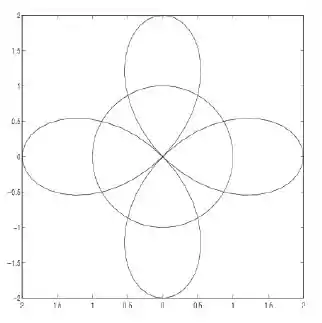
d) O comprimento de arco da rosa de 4 pétalas

Determine o comprimento da astroïde parametrizada por

(a)

(b)

(c)

(d)

(e)

Seja uma parametrização de uma curva no espaço , definida no intervalo , com . Suponha que seja continuamente diferenciável, com derivada denotada por Assinale a alternativa incorreta:

1. Se o comprimento de arco de uma curva é igual a , então , para todo
2. Se para todo , onde é uma constante, então o comprimento de arco da curva é .
3. Se para todo , onde é uma constante, então a curva está contida em uma esfera centrada na origem.
4. Se a curva está contida em uma esfera centrada na origem, então para todo
5. Se para todo , onde são constantes, então a curva é uma reta.

O comprimento de uma curva parametrizada por

É:

Considere a curva

Andando sobre a curva a partir do ponto ao longo de um arco de comprimento igual a , chegaremos ao ponto:

5. Nenhuma das demais alternativas

Seja a curva parametrizada por

1. Reparametriza a curva em relação ao comprimento de arco.
2. Determine o comprimento da curva
3. Seja Determine

Considere a curva parametrizada por , . O comprimento do arco de entre os pontos e é:

a)

b)

c)

d)

e)

Qual o valor de de modo que o comprimento da curva parametrizada por

Seja igual a ?

Qual o valor de de modo que o comprimento da curva parametrizada por

Seja igual a ?

Considere a curva parametrizada por para .

a) Mostre que não é uma parametrização pelo comprimento de arco.

b) Reparametrize a curva pelo comprimento de arco.

Encontre o comprimento da curva de a .

Encontre o comprimento da curva dada pela função vetorial , considerando

Um objeto move-se no espaço , descrevendo uma curva de comprimento . Ele parte do ponto no instante e sua posição ao longo do tempo é dada por . Sua posição final é:

a)

b)

c)

d)

e)

f)

15 - Determine o comprimento das curvas parametrizadas:

c) , , .

Encontre o comprimento de arco da curva

Quando .

Seja e campos vetoriais definidos por:

Seja um ponto localizado na vizinhança de e pertencente à reta que passa por e é paralela à bissetriz dos semieixos cartesianos positivos X e Y. Um engenheiro verificou através de uma aproximação linear partindo do ponto , que o quadrado da norma do campo vetorial em vale . Determine a distância entre os pontos e .

(Capítulo 13.3 – Exercício 3) Determine o comprimento da curva dada.

(Cap. 13.3 - Ex. 5) Determine o comprimento da curva dada.

(Cap. 13.3 - Ex. 14) Reparametrize a curva com relação ao comprimento de arco medido a partir do ponto onde na direção crescente de .

(Cap. 13.3 - Ex. 11) Seja a curva de intersecção do cilindro parabólico e da superfície . Encontre o comprimento exato de da origem até o ponto (6, 18, 36).

Determine o comprimento das curvas parametrizadas:

b) , ,

15 - Determine o comprimento das curvas parametrizadas:

e) , , .

O comprimento da curva parametrizada por , é?

Determine o comprimento do arco da curva cuja equação vetorial é .

Encontre a distância percorrida por uma partícula com posição quando varia em um intervalo de tempo nos itens abaixo. Compare com o comprimento da curva (note que a curva pode ser fechada).

a) , , para

Encontre a distância percorrida por uma partícula com posição quando varia em um intervalo de tempo nos itens abaixo. Compare com o comprimento da curva (note que a curva pode ser fechada).

b) , , para

1) Se é uma função derivável então o comprimento da curva determinada pelo gráfico de é dado pela integral . Calcule esse comprimento em cada um dos casos abaixo.

(b)

(Cap. 13.3 - Ex. 13) Reparametrize a curva com relação ao comprimento de arco medido a partir do ponto onde na direção crescente de .

Calcule o comprimento de arco da curva

2) Seja uma curva no plano definida, parametricamente, por , com . Suponha que e são funções contínuas que não se anulam simultaneamente em e que a curva é percorrida exatamente uma vez quando avança de para . Nessas condições, o comprimento de é dado pela integral definida

Calcule esse comprimento em cada um dos casos abaixo.

(a)

1) Se é uma função derivável então o comprimento da curva determinada pelo gráfico de é dado pela integral . Calcule esse comprimento em cada um dos casos abaixo.

(a)

(Cap. 13.3 - Ex. 2)Determine o comprimento da curva dada.

Uma curva é parametrizada por , . Marque a alternativa correspondente ao comprimento da curva e sua projeção no plano , respectivamente:

1. e semicircunferência de raio .
2. e semicircunferência de raio .
3. e semicircunferência de raio .
4. e semicircunferência de raio .
5. e semicircunferência de raio .

O comprimento da curva dada por , com é:

1) Se é uma função derivável então o comprimento da curva determinada pelo gráfico de é dado pela integral . Calcule esse comprimento em cada um dos casos abaixo.

c) , para

2) Seja uma curva no plano definida, parametricamente, por , com . Suponha que e são funções contínuas que não se anulam simultaneamente em e que a curva é percorrida exatamente uma vez quando avança de para . Nessas condições, o comprimento de é dado pela integral definida

Calcule esse comprimento em cada um dos casos abaixo.

(c)

Dada a curva definida por , .

Determine o comprimento da curva quando varia de até .

A espiral logarítmica é a curva plana definida por .

Calcule o comprimento de arco entre e .

Seja dada a curva

1. Para cada valor do parâmetro , encontre um vetor tangente e um vetor tangente unitário.
2. Encontre o comprimento do arco, , quando o parâmetro varia entre e
3. Reparametrize a curva, agora com o comprimento do arco como novo parâmetro.

Qual o valor de para que o comprimento da hélice parametrizada por

Seja ?

a) Nenhuma das alternativas

b)

c)

d)

e)

2) Seja uma curva no plano definida, parametricamente, por , com . Suponha que e são funções contínuas que não se anulam simultaneamente em e que a curva é percorrida exatamente uma vez quando avança de para . Nessas condições, o comprimento de é dado pela integral definida

Calcule esse comprimento em cada um dos casos abaixo.

(d)

Calcule o comprimento de arco da função , sendo .

Seja uma curva com parametrização e supondo que as coordenadas satisfaçam as equações:

a) Encontre fórmulas explícitas para .

b) Encontre uma parametrização para a reta tangente à curva no ponto

c)Calcule o comprimento do trecho da curva obtido restringindo-se o parâmetro ao intervalo

Considere a curva parametrizada por .

O comprimento de é:

15 - Determine o comprimento das curvas parametrizadas:

f) , , .

Dada a curva

b) Calcule

c) Calcule o comprimento do arco do ponto até .

Determine o comprimento das curvas parametrizadas:

a) , ,

O comprimendo da curva dada pela interseção do cilindro

Com o plano

É:

Considere a curva parametrizada por:

Onde . Sabendo-se que o seu comprimento é , quanto vale ?

a)

b)

c)

d)

e) Nenhuma das alternativas

Calcule o comprimento das curvas dadas:

Calcule o comprimento das curvas dadas:

Calcule o comprimento das curvas dadas:

Calcule o comprimento das curvas dadas: