Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 9.6 - Ex. 6
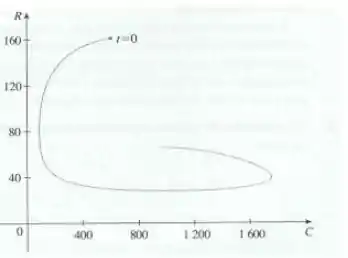
Uma trajetória de fase é mostrada para as populações de coelhos (C) e raposas (R).
- Descreva como cada população muda com o passar do tempo.
- Use sua descrição para fazer um esboço grosseiro dos gráficos de C e R como funções do tempo.
Passo 1
- Inicialmente, quando , tínhamos cerca de 6 coelhos e raposas. Quando , o número de raposas decresce para , enquanto que a população de coelhos está em cerca de
- Agora nós precisamos pegar toda a descrição feita no item (a) e transformá-la em um gráfico, saca só:
Em um tempo , o número de coelhos cresce para e o número de raposas atinge o mínimo, com uma população de mais ou menos .
Agora, em um algum tempo , o número de coelhos cresce mais ainda, parando em cerca de , e o número de raposas cresce apenas um pouquinho, parando em
Em , a população de raposas começa a crescer novamente, parando em cerca de , e a população de coelhos tem uma redução para algo em torno de
Passo 2
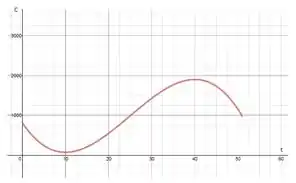
Esse é o gráfico da população dos coelhos com o passar do tempo.
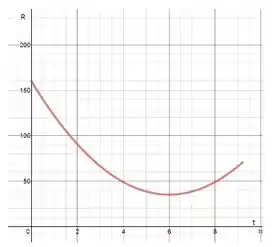
E esse é o gráfico da população de raposas com o passar do tempo.
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Em cada um dos problemas de 7 a 14, verifique se cada função dada é solução da equação diferencial . y ' ' ' + 4 y ' ' ' + 3 y = t , y 1 t = t 3 , y 2 t = e - t + t 3
Em cada um dos problemas de 19 e 20, determine os valores de r para os quais a equação diferencial dada tem uma solução da forma y=t r ,p a r at0 . t 2 y ' ' + 4 t y ' + 2 y = 0
Em cada um dos problemas de 15 a 18, determine os valores de r para os quais a equação diferencial dada tem uma solução da forma y=e r t . y ' ' + y ' - 6 y = 0
Em cada um dos problemas de 7 a 14, verifique se cada função dada é solução da equação diferencial . y ' ' + y = s e c t, 0tπ 2 , y = c o s t ln c o s t + ts e n t
Em cada um dos problemas de 7 a 14, verifique se cada função dada é solução da equação diferencial . y ' ' - y = 0 ,y 1 t = e t , y 2 t = c o s h t