Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.6 - Ex. 68

Usando a função f do exercício 67, calcule

(d)/(d x) ([f (2 sin x)]|_x = pi // 6

Passo 1

Para calcular a derivada dada, vamos usar a regra da cadeia: se tivermos uma função do tipo f (g (x)) então:

(d)/(d x) [f (g (x))] = g^' (x) f^' (g (x))

Passo 2

Assim, para usar a regra da cadeia, vamos fazer g (x) = 2 sin x .

(d)/(d x) [f (2 sin x)] = g^' (x) f^' (g (x)) (d)/(d x) [f (2 sin x)] = (2 cos x) f^' (2 sin x)

Passo 3

Fazendo x = pi // 6 , temos

(d)/(d x) ([f (2 sin x)]|_x = pi // 6 = (2 cos (pi)/(6)) f (2 sin (pi)/(6)) (d)/(d x) ([f (2 sin x)]|_x = pi // 6 = sqrt(3) f (1)

Passo 4

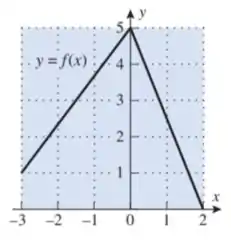
Dessa maneira, precisamos encontrar o valor de f (1) . Note que o gráfico de f para x = 1 é uma reta que passa por (0,5) e (2 , 0) . Assim, a equação da reta será:

f (x) = - (5)/(2) (x - 2) f (x) = - (5)/(2) x + 5

Dessa maneira, para x = 1 , temos

f (1) = - (5)/(2) + 5 = (5)/(2)

Finalmente,

(d)/(d x) ([f (2 sin x)]|_x = pi // 6 = (5 sqrt(3))/(2)

Resposta

(d)/(d x) ([f (2 sin x)]|_x = pi // 6 = (5 sqrt(3))/(2)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = 2 x + 1 5
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = 4 - 3 x 9
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = x 2 - 1 - 10
Escreva as funções na forma y = f ( u ) e u = g ( x ) . Em seguida, determine d y / d x em função de x . y = s e n 3 ( x )
Determine as derivadas das funçõesr = (c o s s e c (theta) + c o t g (theta))^(- 1)