Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.3 - Ex. 23
Use áreas para calcular a integral
Passo 1
Precisamos relacionar a integral dada com a área entre a nossa curva e o eixo X. Precisamos então esclarecer alguns pontos para que possamos resolvê-la. Eles são: os limites do eixo X e qual o comportamento da nossa função neste intervalo.
Passo 2
Vamos começar por determinar o intervalo de análise. O intervalo será dado por , em que é o limite inferior da nossa integral e o limite superior. Desta forma, temos:
Desta forma, temos um limite inferior fixo e um limite superior móvel! Logo, a nossa resposta provavelmente será função de !
Passo 3
A nossa função é . O seu gráfico é o de uma reta que passa pela origem com uma inclinação de . Vejamos abaixo o seu gráfico
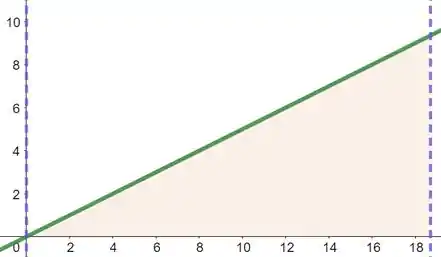
Conforme era esperado, a região entre o eixo X e a nossa função para é um triângulo retângulo.
Passo 4
A base desse triângulo corresponde ao comprimento do intervalo . Desta forma, ela é expressa por:
Já a altura corresponde a interseção da função com a reta . Desta forma, temos:
Agora, só nos falta calcular a área do triângulo. Portanto,
Logo,