Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 23

Use coordenadas polares para determinar o volume do sólido dado.

Uma esfera de raio a .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão, temos que encontrar o volume de uma esfera que possui um raio a . Bom, sabemos que o volume de uma esfera é 4 3 π r 3 , então no nosso caso será: 4 3 π a 3

Mas calma meu amigo, o exercício não está encerrado. Porque temos que encontrar esse valor

utilizando coordenadas polares. Bem, vamos nos lembrar como é a equação de uma esfera centrada na origem?

x 2 + y 2 + z 2 = r 2

Teremos que manipular essa equação para encontrar a função z = f x , y   e transformá-la em coordenadas polares, assim como os limites de integração, após isso é integrar. Simples né? Então vamos comigo.

Passo 2

Em coordenadas retângulares, temos que a equação da esfera é dada por:

x 2 + y 2 + z 2 = r 2

Para converter em coordenadas polares fazemos:

x = r cos ⁡ θ

y = r sen ⁡ θ

Lembrando que o enunciado indica que o raio da nossa esfera é a , ou seja:

x 2 + y 2 + z 2 = a 2

Isolando z para escrever como f ( x , y ) .

z = ± a 2 - x 2 - y 2

Sabemos que x 2 + y 2 = r cos ⁡ θ 2 + r sen ⁡ θ 2 = r 2 , logo:

z = ± a 2 - r 2

Sabemos que o volume do sólido é dado por:

∬ D z d A

Onde D será a região delimitada por:

0 ≤ r ≤ a ,   0 ≤ θ ≤ 2 π

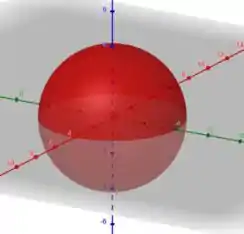
Veja que o limite de integração de 0 até 2 π , não considera a parte inferior da esfera. Essa região delimitada é apenas a metade da esfera que está na parte superior ao plano x y . Aqui teremos que aplicar uma simetria para calcular o volume total, veja no próximo passo.

Passo 3

Agora é só desenvolver. Como:

d A = r d r d θ

Temos que:

z = ± a 2 - r 2

Tente pensar da seguinte forma, a é o raio máximo da esfera, enquanto r é o raio de cada elemento que está sendo calculado. Ou seja, o valor de r varia de 0 até a , que é o valor final do raio.

Por simetria, podemos dizer que o volume total da esfera é duas vezes o volume da parte acima do eixo. Ora, sabemos que a esfera é simétrica em relação sua origem.

z = 2 a 2 - r 2

V = ∬ D z d A = ∫ 0 2 π ∫ 0 a 2 a 2 - r 2 ⋅ r d r d θ

Resolvendo a integral de dentro, temos que aplicar integração por substituição. Chamaremos a 2 - r 2 = t , logo d t = - 2 r d r :

Avaliando os limites de integração, temos:

r = 0 → t = a 2

r = a → t = 0

∫ 0 a 2 a 2 - r 2 ⋅ r d r = ∫ a 2 0 - t d t

- ∫ a 2 0 t 1 2 d t = - 2 t 3 / 2 3 a 2 0

Aplicando os limites de integração temos:

- 2 3 0 3 / 2 - a 2 3 / 2 = 2 3 a 3

Agora que finalizamos a integral “de dentro” temos que colocar esse valor na integral de “fora”.

Logo:

∫ 0 2 π ∫ 0 a 2 a 2 - r 2 ⋅ r d r d θ = ∫ 0 2 π 2 3 a 3 d θ

Resolvendo, agora, temos:

∫ 0 2 π 2 3 a 3 d θ = 2 3 a 3 θ 0 2 π

Aplicando os limites de integração:

2 3 a 3 2 π = 4 π 3 a 3

Portanto o volume vale:

V = 4 π 3 a 3

Resposta

V = 4 π 3 a 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1)Calcular ∬_R^() (x^2 + y^2)^2 d x d y onde R é a região da Figura 7.32.
3) Calcular ∬_R^() (d x d y)/(1 + x^2 + y^2) onde R é a região da Figura 7.34.
5) Usando coordenadas polares, calcular b)int_(- 2)^2 int_(- sqrt(4 - x^2))^(sqrt(4 - x^2)) ( x^2 + y^2 ) d x d y
5) Usando coordenadas polares, calcular int_0^4 int_0^(sqrt(4 y - y^2)) ( x^2 + y^2 ) d x d y
Calcular ∬_R^() e^(2 (x^2 + y^2)) d x d y , sendo R o círculo x^2 + y^2 = 4 .