Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.3 - Ex. 63
- Use a Fórmula (2) para provar que:
- Use a parte (a) anterior, a parte (a) do Exercício 50 na Seção 0.4 e a Regra da Cadeia para mostrar que:
Com
- Conclua da parte (b) que:
Com
Com
Passo 1
(a)
Lembrando que a Fórmula (2) diz que:
No caso dessa questão . Então
Como
Como chegamos numa indeterminação podemos usar a chama da regra de L’Hôpital que está no capítulo 3 seção 6 (3.6) deste livro.
Passo 2
Essa regra diz que se chegarmos numa indeterminação do tipo ou podemos derivar o numerador e o denominador e o valor do limite será mantido.
Aplicando a regra de L’Hôpital ficaremos com a seguinte expressão:
Usando que
Ficamos com a expressão assim:
Agora temos que esse limite que chegamos tem o mesmo valor do limite original, e além disso:
Então chegamos exatamente aonde queríamos provar:
Passo 3
(b)
O Exercício 50 na Seção 0.4 diz que
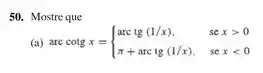
Considerando como verdadeira essa afirmação, vamos derivar as expressões
Pra
Como
Vamos achar que:
Como queria
Passo 4
Agora para
Como é constante sua derivada é zero:
A partir daí a demonstração se torna igual ao caso em que
Então mostramos que de fato vale a relação:
Pra
Passo 5
(c)
Sendo uma função de , basta aplicarmos a regra da cadeia em , usando o resultado da letra (b) chegaremos que
Pra
Resposta
Ei, a resposta está no passo a passo :)