Use um gráfico da sequência para decidir se ela é convergente ou divergente. Se a sequência for convergente, conjecture o valor do limite a partir do gráfico e então demonstre sua conjectura.

Vamos demonstrar com os primeiros termos da sequência como funciona a plotagem do seu gráfico, começando com :

E assim sucessivamente até . Mesmo a sequências sendo infinitas, plotar os 100 primeiros termos já nos dá uma boa ideia de como será seu comportamento.

O gráfico retornado pelo GeoGebra é:

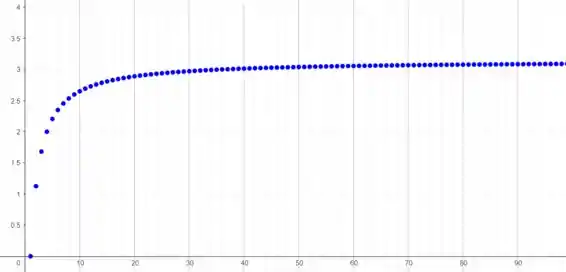
E pronto, já fizemos a primeira parte que dava um medinho, mas que vimos que foi tranquilo.

Ufa! Já passou, mas e agora?

Olhando pro gráfico percebemos que ele depois de um tempo tende a um mesmo valor:

Logo, a série é uma sequência convergente, pois depois de um tempo ela tende a um mesmo valor. Mas que valor será esse?

Pelo gráfico, é um valor um pouco maior do que . Vamos conjecturar que esse valor seja , já que temos uma função trigonométrica e e faz sentido para o que vemos no gráfico.

Será que converge pra ?

Vamos dar uma olhada nesse limite fundamental que usaremos e qual a ideia por trás disso:

Como vimos, se tornarmos nosso limite no mesmo formato que esse, teremos logo seu resultado, pois já é conhecido. Essa é justamente a vantagem de usar limites fundamentais (lembrando que há mais tipos de limites fundamentais, esse é um deles: o limite fundamental trigonométrico).

Agora vamos calcular o limite da sequência pra confirmar nossa hipótese, tá ok?

Vamos fazer uma mudança de variáveis pra tentar chegar no limite fundamental:

Então:

Quando tende a infinito:

O valor de tende a zero, logo nossa série fica da seguinte maneira:

Substituindo os valores para a equação ficar em função de :

Bom, mas o limite dá uma indeterminação:

Logo, vamos aplicar a regra de L’Hopital:

Prontinho! A sequência realmente converge pra .