Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.2 - Ex. 1
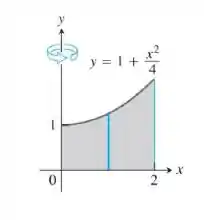
Use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados
Passo 1
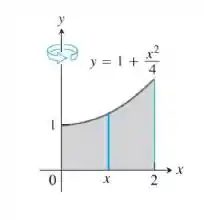
Passo 2
Como a variável de espessura da casca é , os limites de integração para a fórmula da casca são . O volume é portanto,
Retirando a constante e a regra da soma
Usando o Teorema Fundamental do cálculo parte II
Portanto,
Resposta
Exercícios de Livros Relacionados
Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo x da região limitada pelas curvas dadas. Esboce a região e a casca típica. y = 4 x 2 , 2 x + y = 6
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região limitada pelas curvas dadas ao redor dos eixos especificados. Esboce a região e a casca típica. y = x 2 , y = 0 ,
A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método y = x 2 + x - 2 , y = 0 ; ao redor do eixo x
Use a Regra do Ponto Médio com n = 4 para estimar o volume obtido pela rotação ao redor do eixo y da região sob a curva y = t g x , 0 ≤ x ≤ π / 4
A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método. x 2 + y - 1 2 = 1 ; ao redor do eixo x