Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 7
Use o método das cascas cilíndricas para encontrar o volume pela rotação da região delimitada pelas curvas em relação ao eixo dado
Passo 1
Opa, bora resolver essa questão! O enunciado pede pra a gente encontrar o volume do sólido obtido pela rotação da região delimitada pelas seguintes curvas:
Colocando isso em um gráfico temos:
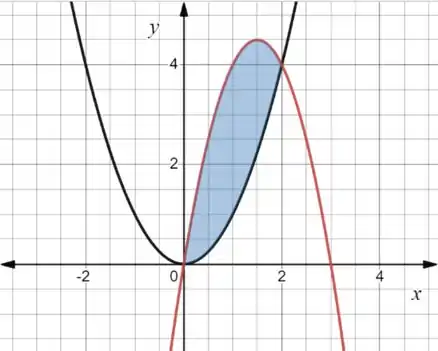
A curva preta é e a vermelha é
Ou seja, essa região azulzinha vai ser rotacionada em torno do eixo . O volume do sólido que a gente obtém é dada por:
O que falta aqui é a gente encontrar e os limites de integração.
Vamos colocar a mão na massa!
Passo 2
Temos que a altura da curva é dada pela diferença entre a amplitude delas, ou seja:
Pra determinar os intervalos de integração vamos calcular as intesecções entre as curvas:
Sendo assim, aplicando método das cascas cilíndricas, obtemos:
Passo 3
Constantes para fora!
Resolvendo a integral:
Prontinho!