Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.8 - Ex. 24
Use o método de Newton para encontrar todas as raízes da equação com precisão de oito casas decimais. Comece fazendo um gráfico para encontrar a aproximação inicial.
Passo 1
Fala, pessoal. Essa questão é sobre o método de Newton, então separa sua calculadora aí 😅!
O enunciado pede para encontrarmos as raízes da equação (com precisão de oito casas decimais)
utilizando o Método de Newton e construindo um gráfico para encontrar a aproximação inicial.
Bem, para facilitar, vamos reescrever a equação dada no enunciado de uma forma mais conveniente (rearrumando os seus termos) da seguinte forma:
Observe que como é dada em função de , então se encontrarmos as raízes da função
ou seja,
e obtermos a raíz quadrada de cada uma dessas raízes, vamos ter as raízes de .
Pensa assim:
certo? Então se é raiz de , ou seja, , vamos ter
Como vamos tomar a raiz quadrada, só precisamos encontrar as raízes positivas de , beleza?
Agora, você se lembra desse tal de método de Newton🤔? Se liga só como ele funciona: Para encontrar as raízes de uma equação , escolhemos um chute inicial , de preferência perto de uma das raízes, e a partir dele formamos uma sequência
e assim por diante:
Se essa sequência convergir, então o limite será uma raiz de .
Para usar esse método e encontrar as raízes de , vamos precisar:
- Encontrar um bom candidato inicial a partir de um gráfico.
- Encontrar a primeira derivada . Para isso, vamos usar a regra da potência
- Para cada raiz de calcular os termos da sequência e encontrar o valor procurado.
Depois que encontrarmos as raízes da função , vamos obter as raízes da função do enunciado, tomando a raiz quadrada delas.
Vamos lá! 💪
Passo 2
A função
é um polinômio de grau , né? Então ele possui até três raízes. Temos que encontrar chutes iniciais para cada raiz de a partir de um gráfico.
Usando uma ferramenta gráfica, obtemos o gráfico abaixo. Para construí-lo você próprio, siga o roteiro para esboçar uma curva dado na seção Seção do Capítulo 4 (ed. 6).
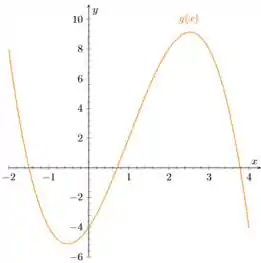
Analisando o gráfico, observe que a função possui três raízes, sendo uma no intervalo , outra no intervalo e mais uma em
Como queremos só as raízes positivas (pois vamos tomar a raiz quadrada) então
temos como boas escolhas iniciais para :
Passo 3
Precisamos calcular a derivada que vamos usar para encontrar os termos da sequência do método de Newton.
Usando a Regra da Potência, temos que a primeira derivada de
é
Agora temos tudo o que precisamos para calcular os termos da sequência e estimarmos cada uma das raízes. Vamos lá!
Passo 4
Vamos começar obtendo a aproximação para a raiz que está no intervalo
Fazendo , então pelo método de Newton temos:
Não esqueça que:
Como
e
então:
Encontrando o terceiro termo !
Como
e
então:
Para o quarto termo , como
e
então:
Ainda não temos que com casas decimais, certo?
Mas observe o seguinte: quando calculamos , temos que
Assim,
Portanto, a primeira raiz de é
Tomando raiz quadrada, encontramos duas raízes para a função original:
Passo 5
Vamos obter a aproximação para a raiz que está no intervalo
Fazendo , então pelo método de Newton temos:
Como
e
então:
Encontrando o terceiro termo !
Como
e
então:
Para o quarto termo , como
e
então:
Ainda não temos que com casas decimais, então vamos calcular o quinto termo !
Como
e
então
Assim como no Passo anterior, observe que quando calculamos , vemos que
Esse valor já pode ser considerado como zero, olhando apenas para as 8 casas decimais.
Assim, a segunda raiz de é :
Tomando raiz quadrada, encontramos duas raízes para a função original:
Resposta
As quatro raízes da equação são e .