Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.4 - Ex. 7
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva.
é a fronteira da região englobada pelas parábolas e
Passo 1
Faaaala galera, tudo na paz?
Precisamos usar o teorema de Green para calcular a seguinte integral de linha com orientação positiva:
Onde, é a fronteira da região englobada pelas parábolas e
O primeiro passo é esboçar essas parábolas. Fazendo isso temos:
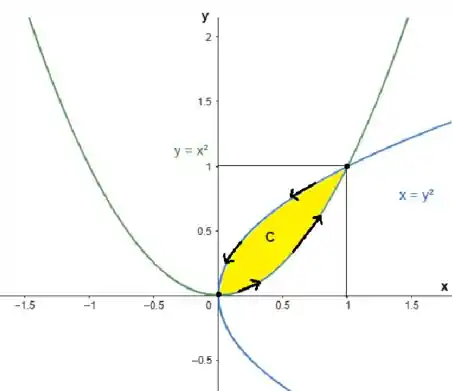
Vamos lembrar do teorema de Green. Para uma curva fechada e orientada positivamente, ou seja, no sentido anti-horário, podemos aplicar:
Nosso desafio agora é determinar os intervalos de integração para e . Olhando para o gráfico podemos adotar a seguinte variação:
Em vai varia de até o encontro das curvas que é . Já em vai variar da curva que esta mais abaixo até a curva mais acima.
Agora seu objetivo vai ser montar a integral e calcular seu valor!
Bora lá!!!
Passo 2
Como é uma curva fechada e orientada positivamente (sentido anti-horário). Isso nos permite aplicar o teorema de Green:
Nossa integral de linha é:
Perceba que:
Aplicando na relação de Green, temos:
Aplicando as derivadas parciais, vamos ficar com:
Passo 3
Agora devemos resolver a integral:
A região limitada por é uma região de limites:
Conforme pode ser visto na imagem:
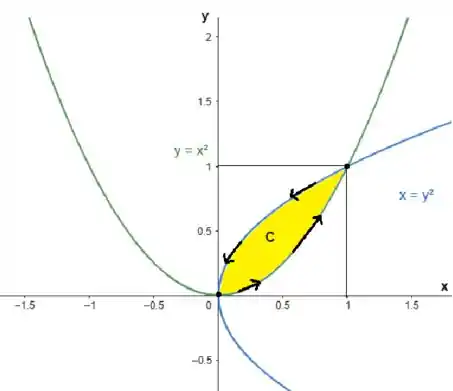
Em vai varia de até o encontro das curvas que é . Já em vai variar da curva que esta mais abaixo até a curva mais acima.
Então, substituindo na integral, temos:
Nesse tipo de situação a ordem de integração é muito importante. Porque um dos integrandos, tem uma função variando, e sempre devemos começar integrando por esses.
Passo 4
Integrando primeiro em , vamos ter:
Aplicando os limites de integração temos:
Agora integrando em relação a , ficamos com:
Aplicando os limites de integração, ficamos com:
Resolvendo vamos ter:
Logo nossa resposta usando o teorema de Green é: