Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 1-f

1 ) Utilizando o teorema de Stokes, transforme a integral

∫ ∫ σ   ∇ × F → ⋅   n →   d S numa integral de linha e calcule.

f )   F → x , y , z = y i → ,       σ é a superfície z =   x 2 + y 2   c o m   z ≤ 1   sendo n → a normal com componente z positiva

Passo 1

Faala ae, beleza??

O exercício pede para usarmos o teorema de Stokes para transforma a integral:

∫ ∫ σ   ∇ × F → ⋅   n →   d S

Em uma integral de linha. Lembrando que o teorema de Stokes diz que:

∫ ∫ S   ∇ × F → ⋅ n →   d S = ∮ ∂ S F → ∙ d r →

Onde ∂ S é a fronteira de S e, também, é um caminho fechado e orientado positivamente.

Passo 2

Beleza! Então, bora olhar para o nosso gráfico:

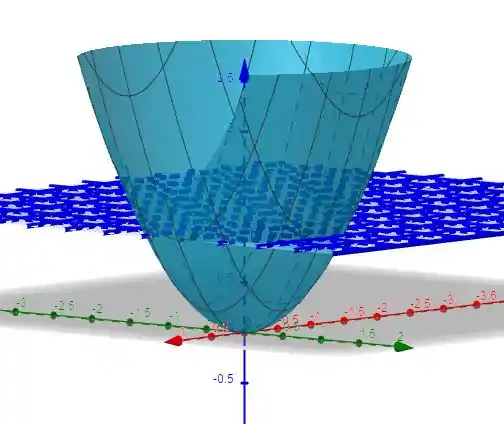
Podemos ver que a interseção do paraboloide com o plano será uma circunferência, mas vamos calculá-la, pois essa será a fronteira da nossa superfície!

Então, substituindo z = 1 no paraboloide:

x 2 + y 2 = 1

Que, realmente, é uma circunferência de raio 1 . Logo, vamos calcular a integral de linha nessa circunferência!

Lembrando que, agora, queremos calcular:

∫ ∂ σ F → x ( t ) , y ( t ) , z ( t ) ∙ σ → ' ( t ) d t

Passo 3

Como já temos o nosso campo F → , só precisamos parametrizar nossa fronteira. E, como nossa fronteira é uma circunferência de raio 1 , podemos parametrizá-la assim:

σ → t = ( cos ⁡ t , sen ⁡ t )

Opa, mas tá faltando o z , certo? Simples! Ele é o z do plano z = 1 :

σ → t = ( cos ⁡ t , sen ⁡ t ,   1 )

Além disso, lembre-se de que precisamos que a curva esteja no sentido positivo, ou seja, anti-horário. Logo, teremos que o parâmetro t varia de 0 a 2 π , beleza?

Pronto! Agora, vamos calcular a derivada dessa parametrização:

σ → ' t = ( - sen ⁡ t , cos ⁡ t , 0 )

Opa, temos tudo para calcular nossa integral de linha!! Então, mãos à obra!

Passo 4

Vamos substituir  F → em função de t na integral de linha. Como F → = y i ^ :

F → t = ( sen ⁡ t , 0 ,   0 )

Substituindo na integral:

∫ 0 2 π sen ⁡ t , 0 ,   0 ∙ ( - sen ⁡ t , cos ⁡ t , 0 ) d t

Fazendo esse produto escalar:

∫ 0 2 π - sen 2 ⁡ t d t

Aqui, vamos usar que:

sen 2 ⁡ t = 1 - cos ⁡ 2 t 2

Assim:

- ∫ 0 2 π 1 - cos ⁡ 2 t 2 d t = - 1 2 ∫ 0 2 π 1 d t - ∫ 0 2 π cos ⁡ 2 t d t

Resolvendo essas integrais, podemos fazer a substituição u = 2 t → d u = 2 d t na segunda integral:

- 1 2 t 0 2 π - 1 2 ∫ 0 4 π cos ⁡ u d u =

- 1 2 2 π - 1 2 sen ⁡ u 0 4 π = - 1 2 2 π - 1 2 0 =

∴

= - π

Prontinho!! Acabamos! 😊

Resposta

∫ ∫ σ   ∇ × F → ⋅   n →   d S = - π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja C a circunferência de raio a , no plano 2 x + 2 y + z = 4 , centrada no ponto 1 ; 2 ; - 2 . Se F x , y , z = y - x; z - x; x - y , determine o valor de a para que: ∮ C Fd r = - 8 3 π .
Calcule ∬ S r o t F →. n →d s Onde F x , y , z = x - x 2 z ; y z 3 - y 2 ; x 2 y - x z e S é qualquer superfície cuja borda seja uma curva fechada no plano x y .
Calcule ∬ S r o t F →. n →d s , onde F x , y , z = 2 x y; 0;- x z e S é a superfície do elipsóide: x 2 4 + y 2 9 + z 2 16 = 1
Calcule ∫ C Fd r , Onde: F x , y , z = e - y - z e - x; e - z - x e - y; e - x - y e - z E C é a curva parametrizada: σ t = ln ⁡ 1 + t ln ⁡ 2; sin ⁡ π t 2; 1 - e t 1 - e Com 0 ≤ t ≤ 1 .
Calcule: ∫ C 2 x y z + sin ⁡ x d x + x 2 z + e y d y + x 2 y + 1 z d z Onde C é a curva parametrizada por: σ t = cos 3 ⁡ t; sin 2 ⁡ t ; t + 1 2 , 0 ≤ t ≤ π .