Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.1 - Ex. 27
Utilize o computador para traçar a curva da equação vetorial dada. Escolha o domínio do parâmetro e ponto de vista de forma a garantir que a visualização é verdadeira.
Passo 1
Olá, meu amigo. Vamos resolver essa atividade?
Vamos utilizar um software matemático para traçar a curva da equação vetorial:
A partir das equações paramétricas, e analisando suas interseções com os planos coordenados podemos descobrir a forma da curva.
Iremos utilizar para essa atividade o GeoGebra 3D, pois é fácil de utilizar, gratuito e online. Mas você pode escolher outro caso se sinta mais confortável.
Podemos garantir uma boa visualização analisando a equação cartesiana da função. Como temos uma função trigonométrica, poderemos utilizar aqui a relação trigonométrica fundamental.
Passo 2
Veja que a nossa parametrização é:
E
No plano , temos uma circunferência de raio 1, pois podemos utilizar a identidade trigonométrica fundamental e a parametrização que nos foi dada:
Porém se analisarmos o eixo , teremos um fator que cresce com o quadrado de , ou seja, de forma não linear.
Termos assim uma hélice que cresce em torno do eixo , delimitada pelo cilindro de base unitária que também cresce em torno de .
Passo 3
Plotando o gráfico com o GeoGebra:
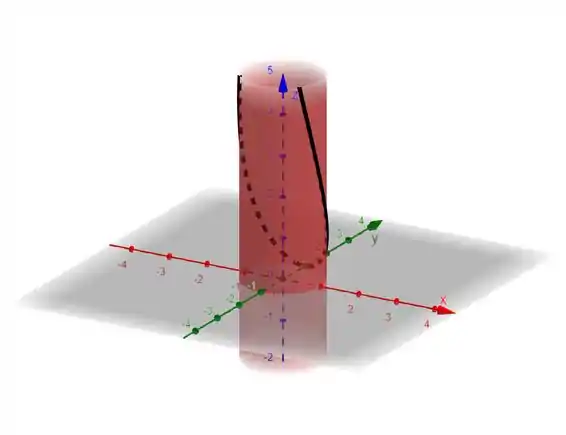
A escolha do intervalo de por acontece pois conseguimos gerar toda a curva dentro desse intervalo, sendo ele o seu período. Veja que de a cobrimos metade da curva, e de a a outra metade.
Resposta
A curva dada é uma hélice em torno do eixo z.