Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.7 - Ex. 25
Utilize um gráfico e/ou curvas de nível para estimar os valores máximos e mínimos locais e pontos de sela da função. Em seguida, use o cálculo para determinar esses valores de modo preciso.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Queremos determinar os valores de máximos, mínimos locais e ponto de sela plotando o gráfico com auxílio de um software.
Lembrando que estamos utilizando o intervalo:
Depois, vamos calcular analiticamente para compararmos os resultados.
Para isso, precisamos fazer as derivadas parciais com relação a e e igualar os seus resultados a zero para encontrarmos os pontos críticos.
Em seguida, iremos fazer as segundas derivadas parciais e aplicar na seguinte expressão (chamada de teste da segunda derivada):
Com isso, a gente analisa as seguinte proposições:
- Se e , então é um mínimo local;
- Se e , então é um máximo local;
- Se , não é nem máximo e nem mínimo local.
Depois, deveremos determinar também os pontos de sela da função. Nesse caso, estamos referindo a última das proposições que acabamos de falar!!
Em outras palavras, se para um ponto , então esse ponto é o nosso ponto de sela da função! Vai ser nesse ponto em que o gráfico da função cruza o plano tangente em .
Por fim, iremos utilizar uma ferramenta gráfica para plotar o gráfico!!
😉
Passo 2
Primeiramente plotando o gráfico em várias perspectivas, temos:
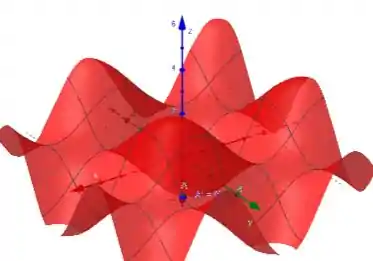
Assim, analisando as figuras, percebemos que o ponto de máximo ocorre em:
E o ponto de mínimo em:
E o ponto de sela em:
Agora vamos aos cálculos!!!
Passo 3
Vamos fazer as derivadas parciais de , a começar por :
Fazendo o como constante e derivando , temos:
Agora vamos para :
Fazendo o como constante e derivando , temos:
Igualando ambas equações a zero e colocando num sistema, obtemos:
Resolvendo o sistema, obtemos os seguintes pontos críticos:
Agora vamos para as derivadas segundas!!
Passo 4
Vamos fazer . Para isso, basta derivarmos com relação a :
Agora vamos fazer . Para isso, basta derivarmos com relação a :
Por fim, vamos fazer . Para isso, basta derivarmos com relação a :
Agora é só substituir na expressão de !! Bora lá!!
Passo 5
Sabemos que:
Assim, substituindo pelas expressões que encontramos, obtemos:
Substituindo os valores de por , obtemos:
Aqui a gente não pode inferir nada.
Passo 6
Agora, substituindo os valores de por , obteremos:
Se substituirmos por em , encontraremos um valor tal que
Assim, temos um máximo local em:
Passo 7
Agora, substituindo os valores de por , obteremos:
Se substituirmos por em , encontraremos um valor tal que
Assim, temos um máximo local em:
Veja que os resultados coincidem com os que estimamos no gráfico no passo 2!!! 😉
Resposta
Demonstração